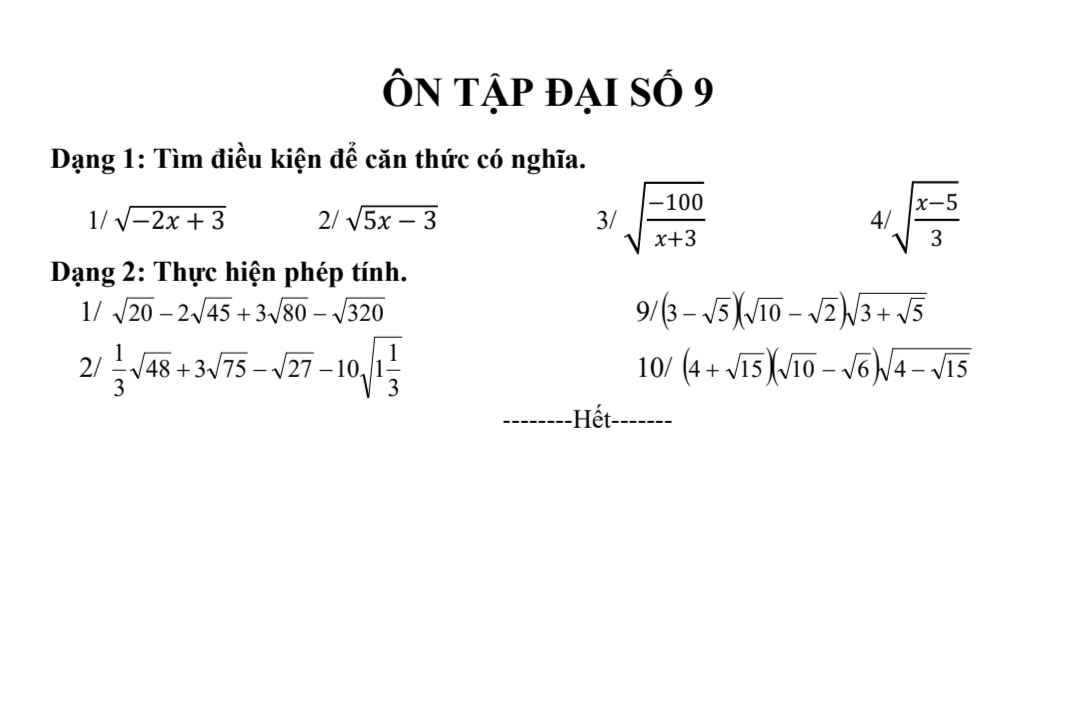
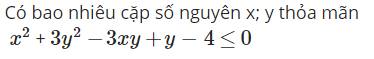Câu 2:
\(=\sqrt{5}-20\sqrt{5}+\sqrt{5}-2=-18\sqrt{5}-2\)
1.
ĐKXĐ: \(x>0;x\ne1\)
\(M=\left(\dfrac{\sqrt[]{x}}{\sqrt[]{x}+1}+\dfrac{\sqrt[]{x}}{\sqrt[]{x}-1}\right):\left(\dfrac{3\sqrt[]{x}}{x-1}\right)\)
\(=\left(\dfrac{\sqrt[]{x}\left(\sqrt[]{x}-1\right)+\sqrt[]{x}\left(\sqrt[]{x}+1\right)}{\left(\sqrt[]{x}+1\right)\left(\sqrt[]{x}-1\right)}\right).\left(\dfrac{x-1}{3\sqrt[]{x}}\right)\)
\(=\left(\dfrac{x-\sqrt[]{x}+x+\sqrt[]{x}}{x-1}\right)\left(\dfrac{x-1}{3\sqrt[]{x}}\right)\)
\(=\dfrac{2x\left(x-1\right)}{\left(x-1\right).3\sqrt[]{x}}=\dfrac{2\sqrt[]{x}}{3}\)
b.
\(M< 1\Rightarrow\dfrac{2\sqrt[]{x}}{3}< 1\)
\(\Rightarrow\sqrt[]{x}< \dfrac{3}{2}\)
\(\Rightarrow x< \dfrac{9}{4}\)
Kêt hợp ĐKXD ta được: \(\left\{{}\begin{matrix}0< x< \dfrac{9}{4}\\x\ne1\end{matrix}\right.\)






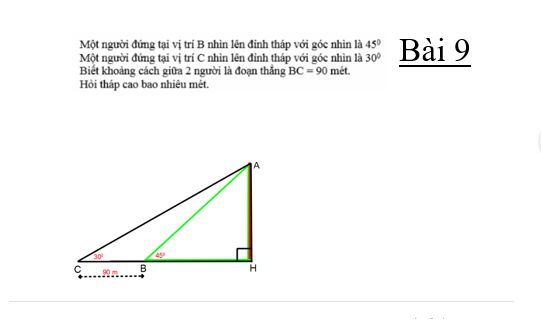 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ