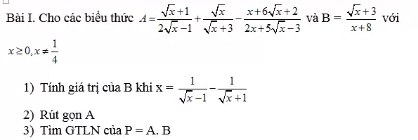Question

Giúp em với ạ em cần câu b, c

Answer 1

b.

Do tam giác ABC vuông tại A \(\Rightarrow CA\perp BD\)

Theo giả thiết \(BK\perp CK\) hay \(BK\perp CD\)

Mà CA và BK cắt nhau tại H

\(\Rightarrow H\) là trực tâm tam giác BCD

\(\Rightarrow DH\) là đường cao thứ 3 

\(\Rightarrow DH\perp BC\) tại E

\(\Rightarrow\widehat{DEC}=90^0\)

\(\Rightarrow\widehat{HDK}=\widehat{CBK}\) (cùng phụ \(\widehat{BCD}\))

Xét hai tam giác DKH và tam giác BKC có:

\(\left\{{}\begin{matrix}\widehat{HDK}=\widehat{CBK}\left(cmt\right)\\\widehat{DKH}=\widehat{BKC}=90^0\end{matrix}\right.\)

\(\Rightarrow\Delta DKH\sim\Delta BKC\left(g.g\right)\)

\(\Rightarrow\widehat{DHK}=\widehat{BCK}\) (1)

Trong tam giác vuông DKH:

\(sin\widehat{DHK}=\dfrac{DK}{DH}\Rightarrow DK=DH.sin\widehat{DHK}\) (2)

(1);(2) \(\Rightarrow DK=DH.sin\widehat{BCK}\)

 

Answer 2

c,

Câu này có nhiều cách giải (dựng thêm hình hoặc chứng minh BAE và BCD đồng dạng).

Từ E kẻ \(EF\perp AB\)

Xét hai tam giác BED và BAC có:

\(\left\{{}\begin{matrix}\widehat{BED}=\widehat{BAC}=90^0\\\widehat{B}-chung\end{matrix}\right.\)

\(\Rightarrow\Delta BED\sim\Delta BAC\left(g.g\right)\)

\(\Rightarrow\dfrac{BE}{BA}=\dfrac{BD}{BC}\Rightarrow BE=\dfrac{BA.BD}{BC}=\dfrac{2.3}{4}=\dfrac{3}{2}\left(cm\right)\)

Do EF song song AC (cùng vuông góc AB), áp dụng định lý Thales:

\(\dfrac{EF}{AC}=\dfrac{BE}{BC}\Rightarrow EF=\dfrac{BE.AC}{BC}=\dfrac{\dfrac{3}{2}.2\sqrt{3}}{4}=\dfrac{3\sqrt{3}}{4}\left(cm\right)\)

\(\Rightarrow S_{\Delta ABE}=\dfrac{1}{2}EF.AB=\dfrac{1}{2}.\dfrac{3\sqrt{3}}{4}.2=\dfrac{3\sqrt{3}}{4}\left(cm^2\right)\)

Answer 3