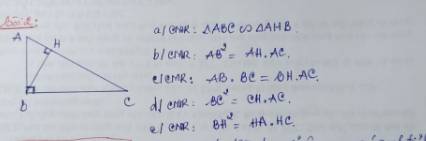Question

giúp  em nhanh với ạ 

Answer 1

a) Xét hai tam giác vuông: \(\Delta ABC\) và \(\Delta AHB\) có:

\(\widehat{A}\)  chung

\(\Rightarrow\Delta ABC\sim\Delta AHB\) (g-g)

b) Do \(\Delta ABC\sim\Delta AHB\) (cmt)

\(\Rightarrow\dfrac{AB}{AH}=\dfrac{AC}{AB}\)

\(\Rightarrow AB^2=AH.AC\)

c) Xét hai tam giác vuông: \(\Delta ABC\) và \(\Delta BHC\) có:

\(\widehat{C}\) chung

\(\Rightarrow\Delta ABC\sim\Delta BHC\) (g-g)

\(\Rightarrow\dfrac{AB}{BH}=\dfrac{AC}{BC}\)

\(\Rightarrow AB.BC=BH.AC\)

d) Do \(\Delta ABC\sim\Delta AHB\) (cmt)

\(\Delta ABC\sim\Delta BHC\) (cmt)

\(\Rightarrow\Delta AHB\sim\Delta BHC\)

\(\Rightarrow\dfrac{AH}{BH}=\dfrac{BH}{HC}\)

\(\Rightarrow BH^2=AH.HC\)

Answer 2

a: Xét ΔHAB vuông tại H và ΔBAC vuông tại B có

góc A chung

=>ΔHAB đồng dạng với ΔBAC

b: ΔHAB đồng dạng với ΔBAC

=>HA/BA=AB/AC=HB/BC

=>AB^2=AH*AC

c: HB/BC=AB/AC

=>HB*AC=BA*BC

d,e: ΔACB vuông tại B có BH là đường cao

nên BC^2=CH*CA và BH^2=HA*HC