Tập xác định D = R.
Giải từng bất phương trình:
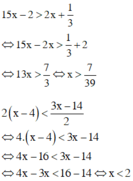
Vậy tập nghiệm của hệ bất phương trình là
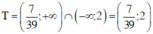
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tập xác định D = R.
Giải từng bất phương trình:
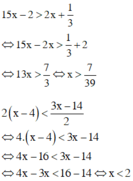
Vậy tập nghiệm của hệ bất phương trình là
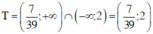
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
cặp số (-1;2) là nghiệm của bất phương trình nào sau đây?
a) 2x - y +3 > 0 c) x - y - 15 < 0
b) -x + 2 + 2(y - 2) < 2(2 - x) d) 3(x - 1) + 4(y - 2) < 5x - 3
Giải các bất phương trình sau
1) \(\sqrt{2+x}+\sqrt{7-x}+\sqrt{-x^2+5x+14}< 3\) <3
2) \(x^2+2x+\sqrt{\left(x+3\right)\left(1-x\right)+5}>2\)
Giải các phương trình, bất phương trình sau:
1) \(\sqrt{3x+7}-5< 0\)
2) \(\sqrt{-2x-1}-3>0\)
3) \(\dfrac{\sqrt{3x-2}}{6}-3=0\)
4) \(-5\sqrt{-x-2}-1< 0\)
5) \(-\dfrac{2}{3}\sqrt{-3-x}-3>0\)
- giải các bất phương trình sau:
a) (\(3x^2-7x+4\))(\(x^2+x+4\))\(>0\)
b) \(x^3-13x^2+42x-36>0\)
c) \(x\left(x+5\right)\le2\left(x^2+2\right)\)
Giải bất phương trình: \(\sqrt[3]{x+1}+\sqrt{2x+4}< 3-x\sqrt{2}\)
Cứu
Giải bất phương trình \(\dfrac{3-3x}{-x^2-2x+15}-1\ge0\)
Giải hệ phương trình
\(\hept{\begin{cases}x^3-x^2y=x^2-x+y+1\\x^3-9y^2+6\left(x-3y\right)-15=3\sqrt[3]{6x^2+2}\end{cases}}\)
\(\left(x-2\right)\sqrt{x^2-2x-3}\le x^2-4\)
Giải bất phương trình
Giải các bất phương trình sau:
a)\(\left(x^2+3x-4\right)\left(3-2x\right)\)<0
b) \(\dfrac{x^2+3x+4}{x^2-2}\ge0\)
c) \(\dfrac{x\left(x^2+4x+4\right)}{x^2-1}\ge0\)