Câu 4:
a: Phương trình hoành độ giao điểm là:
\(x^2+x-6=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-2\right)=0\)
=>x=-3 hoặc x=2
Khi x=-3 thì y=9
Khi x=2 thì y=4
Vậy: M(-3;9) N(2;4)
b: \(OM=\sqrt{\left(-3\right)^2+9^2}=3\sqrt{10}\)
\(ON=\sqrt{2^2+4^2}=2\sqrt{10}\left(cm\right)\)
\(MN=\sqrt{\left(2+3\right)^2+\left(4-9\right)^2}=5\sqrt{2}\left(cm\right)\)
Vì \(ON^2+MN^2=OM^2\)
nên ΔONM vuông tại N
=>\(S_{OMN}=\dfrac{2\sqrt{10}\cdot5\sqrt{2}}{2}=5\sqrt{20}=10\sqrt{5}\)
4.a) bạn tự làm nha
b) từ M kẻ đường vuông góc với trục hoành tại P, MN cắt trục hoành tại E kẻ NH vuông góc với trục hoành tại H
ta có M(-3;9) => MP = 9 và OP = \(\left|-3\right|\)
=> diện tích tam giác PMO = \(\dfrac{9.3}{2}\) = 13,5 (đvcd )2
có N(2;4) => NH = 4 và OE = 6
=> diện tích tam giác ONE = \(\dfrac{4.6}{2}\) = 12 (đvcd)2
có PE = OE + OP => \(\left|-3\right|\) + 6 = 9
vậy diện tích tam giác MPE = \(\dfrac{9.9}{2}\) = 40,5 ( đvcd )2
vậy diện tích tam giác MNO = diện tích tam giác MPE - ( diện tích tam giác MOP + diện tích tam giác ONE )
=> diện tích tam giác MNO = 40,5 - ( 13,5 + 12 )
= 15 (đvcd)^2
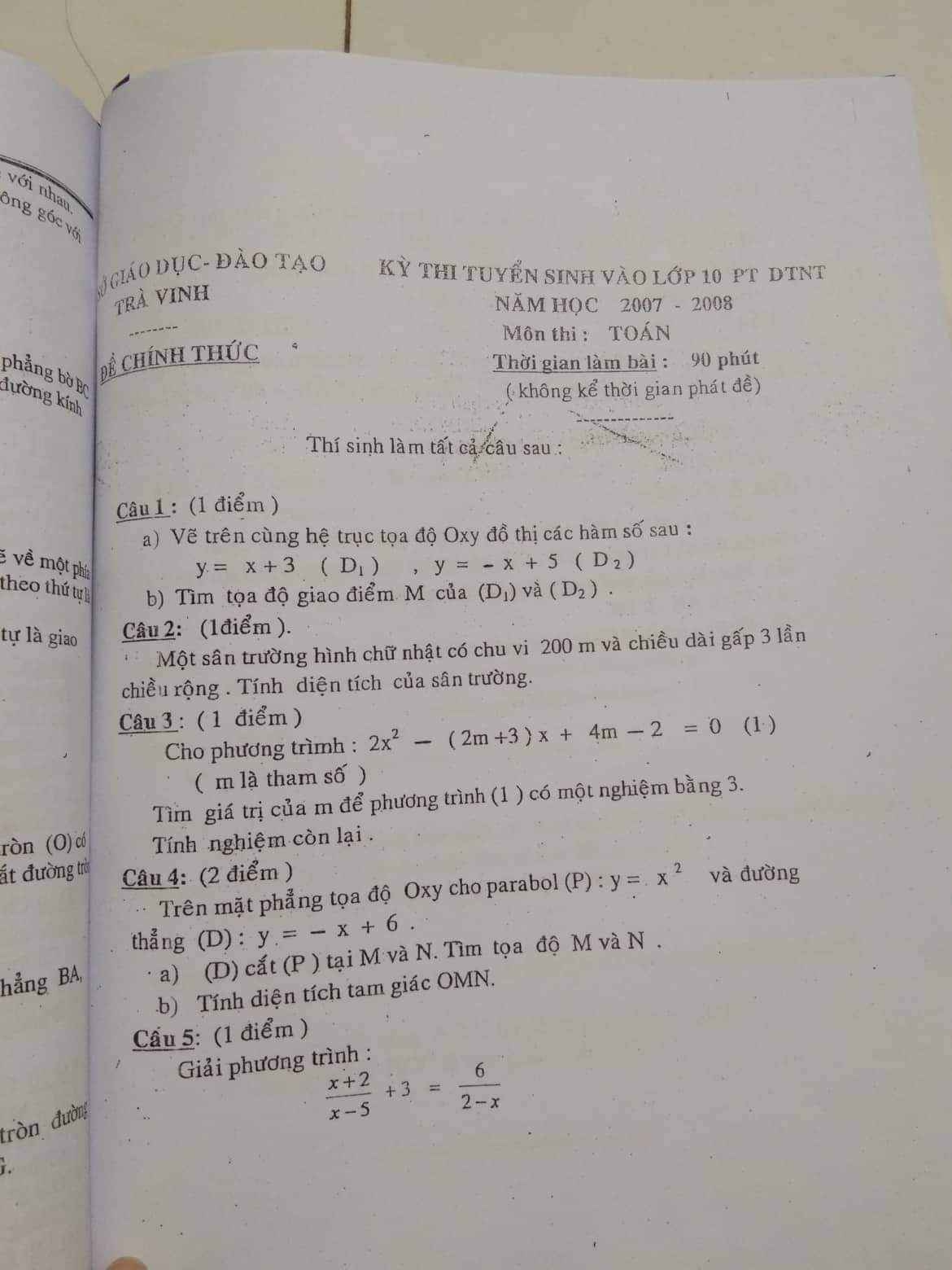
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
