=>sin 5x=sin(pi/2-x)
=>5x=pi/2-x+k2pi hoặc 5x=pi/2+x+k2pi
=>6x=pi/2+k2pi hoặc 4x=pi/2+k2pi
=>x=pi/12+kpi/3 hoặc x=pi/8+kpi/2
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
giải phương trình lượng giác Sin(cosx)=1
Nghiệm của phương trình
1
2
.
sin
x
.
cos
x
0
là
Đọc tiếp
Nghiệm của phương trình 1 2 . sin x . cos x = 0 là
TT
2 tháng 8 2019 lúc 11:45
Gải phương trình:
\(\sin\left(x\right)^3.2+\cos\left(2x\right)^3+\frac{1}{2}\sin\left(4x\right)=1\)
Giải phương trình:
1,\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
2,\(|cosx-sinx|+2sin2x=1\)
3,\(2sin2x-3\sqrt{6}|sinx+cosx|+8=0\)
4,\(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\)
Giải phương trình:
\(\dfrac{1+cos2x\times cosx}{cos^2x}+2\left(sin^4x+cos^4x\right)=3\)
Tìm m để phương trình sin
2
x
+
5
π
2
-m cosx +1 0 có đúng 3 nghiệm trên
(
0
;
4
π
3
]
A. -2
≤
m
≤
-1 B. -2
m
≤
-
1...
Đọc tiếp
Tìm m để phương trình sin 2 x + 5 π 2 -m cosx +1 = 0 có đúng 3 nghiệm trên ( 0 ; 4 π 3 ]
A. -2 ≤ m ≤ -1
B. -2 < m ≤ - 1
C. -2 ≤ m < - 1
D. -2 ≤ m
Giaỉ các phương trình lượng giác sau:
1. sin(sinx)=0
2. sin(cosx)=0
3. \(\sqrt{3}\sin-\cos x=2cos3x\)
4. \(\sin2x=sin\left(2x-\dfrac{\pi}{2}\right)\)
5. \(4\cos\left(3\pi-2x\right)=\sqrt{2}\)
Tính tổng S là tổng các nghiệm thuộc đoạn
0
,
2
π
của phương trình:
sin
2
x
+
9
π
2
-
3
.
cos...
Đọc tiếp
Tính tổng S là tổng các nghiệm thuộc đoạn 0 , 2 π của phương trình: sin 2 x + 9 π 2 - 3 . cos x - 15 π 2 = 1 + 2 . sin x
Biến đổi phương trình sau cos3x-sinx
3
(cosx-sin3x) về dạng sin(ax+b)sin(cx+d) với b, d thuộc khoảng
-
π
2
;
π
2
. Tính chính xác giá trị của b+d ?
Đọc tiếp
Biến đổi phương trình sau cos3x-sinx= 3 (cosx-sin3x) về dạng sin(ax+b)=sin(cx+d) với b, d thuộc khoảng - π 2 ; π 2 . Tính chính xác giá trị của b+d ?
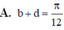
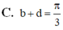
