Các câu hỏi tương tự
Cho . Giá trị nhỏ nhất của biểu thức
là
Nhập kết quả dưới dạng số thập phân gọn nhất.
Cho phương trình
x
3
−
3
x
2
+
1
−
m
0
1
.
Điều kiện của tham số m để phương trình (1) có ba nghiệm phân biệt thỏa mãn
x
1
1
x
2
x
3
là A.
m
−...
Đọc tiếp
Cho phương trình x 3 − 3 x 2 + 1 − m = 0 1 . Điều kiện của tham số m để phương trình (1) có ba nghiệm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 là
A. m = − 1
B. − 1 < m < 3
C. − 3 < m < − 1
D. − 3 ≤ m ≤ − 1
Cho phương trình
4
x
(
m
+
1
)
2
x
+
m
0
.Điều kiện của m để phương trình có đúng 3 nghiệm phân biệt là: A.
m...
Đọc tiếp
Cho phương trình 4 x = ( m + 1 ) 2 x + m = 0 .Điều kiện của m để phương trình có đúng 3 nghiệm phân biệt là:
A. m ≥ 1
B. m > 1
C. m > 0 v à m ≠ 1
D. m > 0
Tìm x, y thỏa mãn:
Trả lời: (x;y)=()
(Nhập kết quả x trước và y sau dưới dạng số thập phân gọn nhất ngăn cách nhau bởi dấu “;”)
Điều kiện của tham số m để phương trình
m
sin
x
−
3
cos
x
5
có nghiệm là A.
−
4
≤
m
≤
4
B.
m
≥
4
C.
m
≥
34
D.
m
≤
−
4...
Đọc tiếp
Điều kiện của tham số m để phương trình m sin x − 3 cos x = 5 có nghiệm là
A. − 4 ≤ m ≤ 4
B. m ≥ 4
C. m ≥ 34
D. m ≤ − 4 m ≥ 4
Cho hàm số y = f(x) có đồ thị như hình bên. Khi đó điều kiện đầy đủ của m để phương trình f(x) = m có bốn nghiệm thực phân biệt là
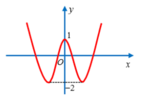
A. m ≤ − 2.
B. -2 < m < 1
C. m = 1
D. m > 1
Điều kiện của tham số m để phương trình
8
log
3
x
-
3
x
log
3
2
m
có nhiều hơn một nghiệm là A.
m
-
2
B.
m...
Đọc tiếp
Điều kiện của tham số m để phương trình 8 log 3 x - 3 x log 3 2 = m có nhiều hơn một nghiệm là
A. m < - 2
B. m > 2
C. - 2 < m < 0
D. - 2 < m < 2
Cho tam giác ABC vuông tại A, có AB=5cm và BC=10cm. Gọi M, N, P lần lượt là trung điểm
của các cạnh AB, BC, CA. Chu vi đường tròn ngoại tiếp tam giác MNP là ......?..cm
(Nhập kết quả dưới dạng số thập phân làm tròn đến 1 chữ số sau dấu “,”)
Cho hàm số yf(x) có đồ thị như hình vẽ bên:Điều kiện của m để phương trình
f
x
m
có 4 nghiệm phân biệt
x
1
,
x
2
,
x
3
,
x
4
thỏa mãn
x...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên:
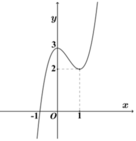
Điều kiện của m để phương trình f x = m có 4 nghiệm phân biệt x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 ≤ - 1 2 x 2 < x 3 ≤ 1 2 x 4 là:
A. m ∈ 2 ; 3
B. m ∈ 2 ; 3
C. m ∈ [ 5 2 ; 3 )
D. m ∈ [ 2 ; 5 2 )
