Đáp án D
Phương trình có nghiệm ⇔ m 2 + 3 2 ≥ 5 2 ⇔ m 2 ≥ 16 ⇔ m ≤ − 4 m ≥ 4
Đúng 0
Bình luận (0)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Tổng tất cả các giá trị nguyên của m để phương trình
4
sin
x
+
(
m
-
4
)
cos
x
-
2
m
+
5
0
có nghiệm là: A. 5 B. 6 C. 10 D. 3
Đọc tiếp
Tổng tất cả các giá trị nguyên của m để phương trình 4 sin x + ( m - 4 ) cos x - 2 m + 5 = 0 có nghiệm là:
A. 5
B. 6
C. 10
D. 3
Số giá trị nguyên m để phương trình
4
m
-
4
.
sin
x
.
cos
x
+
m
-
2
.
cos
2
x
3
m
-
9
. Có nghiệm là: A. 7 B. 6 C. 5 D. 4
Đọc tiếp
Số giá trị nguyên m để phương trình 4 m - 4 . sin x . cos x + m - 2 . cos 2 x = 3 m - 9 . Có nghiệm là:
A. 7
B. 6
C. 5
D. 4
Tham số m để phương trình
3
sin
x
+
m
cos
x
5
vô nghiệm A.
m
∈
(
-
∞
;
-
4
]
∪
[
4
;
+
∞
)
B.
m
∈
(
4
;
+
∞
)
C.
m
∈
(
-...
Đọc tiếp
Tham số m để phương trình 3 sin x + m cos x = 5 vô nghiệm
A. m ∈ ( - ∞ ; - 4 ] ∪ [ 4 ; + ∞ )
B. m ∈ ( 4 ; + ∞ )
C. m ∈ ( - 4 ; 4 )
D. m ∈ ( - ∞ ; - 4 )
Cho bất phương trình
m
.
3
x
+
1
+
(
3
m
+
2
)
(
4
-
7
)...
Đọc tiếp
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Số giá trị nguyên của tham số m thuộc đoạn
[
-
2019
;
2019
]
để phương trình
x
2
+
(
m
+
2
)
x
+
4
(
m
-
1
)
x
3
+
4
x
có nghiệm là A. 2011. B. 2012. C. 2013. D. 2014.
Đọc tiếp
Số giá trị nguyên của tham số m thuộc đoạn [ - 2019 ; 2019 ] để phương trình x 2 + ( m + 2 ) x + 4 = ( m - 1 ) x 3 + 4 x có nghiệm là
A. 2011.
B. 2012.
C. 2013.
D. 2014.
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
a
,
b
,
c
,
d
∈
ℝ
)
có bảng biến thiên như hình sau:Tìm tất cả giá trị thực của tham số m để phương trình
m
f...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c , d ∈ ℝ ) có bảng biến thiên như hình sau:
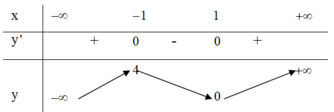
Tìm tất cả giá trị thực của tham số m để phương trình m = f ( x ) có 4 nghiệm phân biệt trong đó có đúng một nghiệm dương.
A.m > 2
B.0 < m < 4
C.m > 0
D.2 < m < 4
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m
+
3
.
m
+
cos
x
3
3
cos
x
có nghiệm thực? A. 2. B. 7. C. 5. D. 3.
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m + 3 . m + cos x 3 3 = cos x có nghiệm thực?
A. 2.
B. 7.
C. 5.
D. 3.
Cho phương trình
(
x
+
x
+
1
)
(
m
x
+
1
+
1
x
+
16
x
2...
Đọc tiếp
Cho phương trình ( x + x + 1 ) ( m x + 1 + 1 x + 16 x 2 + x 4 ) = 1 với m là tham số thực. Tìm số các giá trị nguyên của m để phương trình có hai nghiệm thực phân biệt
A. 3.
B. 4.
C. 5.
D. 6
Biết điều kiện cần và đủ của m để phương trình
log
2
1
2
x
-
2
2
+
4
m
-
5
log
1
2
1
x
-...
Đọc tiếp
Biết điều kiện cần và đủ của m để phương trình log 2 1 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 - 8 m - 4 = 0 . Có nghiệm thuộc 5 4 ; 4 là m ∈ a ; b . Tính T=a+b
A. 10 3
B. 4
C. -4
D. - 10 3
Cho hàm số yf(x) có đồ thị như hình vẽ bên:Điều kiện của m để phương trình
f
x
m
có 4 nghiệm phân biệt
x
1
,
x
2
,
x
3
,
x
4
thỏa mãn
x...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên:
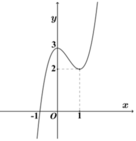
Điều kiện của m để phương trình f x = m có 4 nghiệm phân biệt x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 ≤ - 1 2 x 2 < x 3 ≤ 1 2 x 4 là:
A. m ∈ 2 ; 3
B. m ∈ 2 ; 3
C. m ∈ [ 5 2 ; 3 )
D. m ∈ [ 2 ; 5 2 )