ĐK: x ≥ 0
pt <=> 4x - 4√x +1 + x - 2√x .y + y^2 = 0
<=> (2√x -1)² + (√x -y)² = 0
(a² + b² = 0 <=> a và b bằng 0)
<=> hệ 2√x -1 = 0, √x -y = 0
<=> x = 1/4, y =1/2 (thỏa mãn)
KL: x=1/4, y = 1/2
tkss nhiều, bn giúp mik giải vài câu nữa đc k
ĐK: x ≥ 0
pt <=> 4x - 4√x +1 + x - 2√x .y + y^2 = 0
<=> (2√x -1)² + (√x -y)² = 0
(a² + b² = 0 <=> a và b bằng 0)
<=> hệ 2√x -1 = 0, √x -y = 0
<=> x = 1/4, y =1/2 (thỏa mãn)
KL: x=1/4, y = 1/2
tkss nhiều, bn giúp mik giải vài câu nữa đc k
Tập hợp các giá trị nguyên x thỏa mãn (với p là số nguyên tố)
là {}
Nhập kết quả theo thứ tự tăng dần ngăn cách nhau bởi dấu “;”
Tập hợp các giá trị nguyên x thỏa mãn (với p là số nguyên tố)
là {}
Nhập kết quả theo thứ tự tăng dần ngăn cách nhau bởi dấu “;”
Cho . Giá trị nhỏ nhất của biểu thức
là
Nhập kết quả dưới dạng số thập phân gọn nhất.
Điều kiện của để hệ phương trình
có nghiệm
mà
là m <
(Nhập kết quả dưới dạng số thập phân gọn nhất)
Hình phẳng (H) được giới hạn bởi đồ thị của hai hàm số đa thức bậc bốn y=f(x) và y=g(x). Biết rằng đồ thị của hai hàm số này cắt nhau tại đúng ba điểm phân biệt có hoành độ lần lượt là −3;−1;2. Diện tích của hình phẳng (H) (phần gạch sọc trên hình vẽ bên) gần nhất với kết quả nào dưới đây?
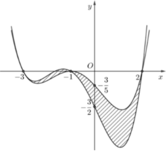
A.3,11
B. 2,45
C. 3,21
D. 2,95
Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn: S A 2 + B C 2 = 18 và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng: V m a x = x y 4 ; x , y ∈ ℕ * ; x , y = 1. Khi đó: x, y thỏa mãn bất đẳng thức nào dưới đây?
A. x + y 2 − x y > 4550.
B. x y + 2 x y > 2550.
C. x 2 − x y + y 2 < 5240.
D. x 3 − y > 19602.
Cho hai số phức a và b thỏa mãn a = b = 1 . So sánh hai số x = a + b + i ; y = a b + i a + b ta thu được kết quả nào trong các kết quả sau?
A. x = y
B. x < y
C. x > y
D. Kết quả khác
Cho hàm số y = f(x) có đạo hàm trên ℝ , thỏa mãn f − 1 = f 3 = 0 và đồ thị của hàm số y = f ' x có dạng như hình dưới đây.
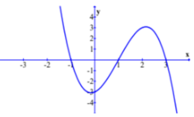
Hàm số y = f x 2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (1;2)
B. (-2;1)
C. (0;4)
D. (-2;2)