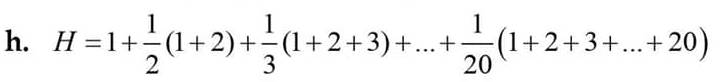\(H=1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+...+\dfrac{1}{20}\left(1+2+3+...+20\right)\)
\(=1+\dfrac{1}{2}\cdot\dfrac{2\cdot3}{2}+\dfrac{1}{3}\cdot\dfrac{3\cdot4}{2}+...+\dfrac{1}{20}\cdot\dfrac{20\cdot21}{2}\)
\(=1+\dfrac{3}{2}+\dfrac{4}{2}+...+\dfrac{21}{2}\)
\(=\dfrac{2+3+4+...+21}{2}\)
\(=\dfrac{\left(21+2\right)\cdot\dfrac{\left(21-2+1\right)}{2}}{2}=\dfrac{23\cdot20}{4}=23\cdot5=115\)