#\(N\)
`a,` `GT: AB = AC,` \(\widehat{B}=\widehat{C}\)
`CM: BB' = C``C'`
`BB'` là đường trung tuyến
`-> B'` là trung điểm của `AC`
`-> AB' = B'C`
`C``C'` là đường trung tuyến
`-> C'` là trung điểm của `AB`
`-> AC' = C'B`
Tam giác `ABC` cân tại `A`
`-> AB = AC`
`-> AC' = AB' = C'B = B'C`
Xét Tam giác `BB'C` và Tam giác `C``C'B:`
`C'B = B'C`
\(\widehat{B}=\widehat{C}\)
`BC` chung
`=>` Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`
`=> BB' = C``C' (2` cạnh tương ứng `) (đpcm)`
`b, GT: AB' = B'C ; AC'=C'B ; C``C' = BB'`
`KL:` Tam giác `ABC` cân
`BB', C``C'` là đường trung tuyến
giả sử: `BB'` cắt `C``C'` tại `G`
`-> G` là trọng tâm của Tam giác `ABC`
`-> GB = 2/3 BB'`
`-> GC = 2/3 C``C'`
`BB' = C``C' -> GB = GC`
`->` Tam giác `GBC` cân tại `G`
`->`\(\widehat{B_1}=\widehat{C_1}\)
Xét Tam giác `BB'C` và Tam giác `C``C'B` có:
`BB' = C``C'`
\(\widehat{B_1}=\widehat{C_1}\)
`BC` chung
`=>`Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`
`-> BC' = B'C`
`-> 1/2 AB = 1/2 AC`
`-> AB = AC`
`->` Tam giác `ABC` cân tại `A (đpcm)`.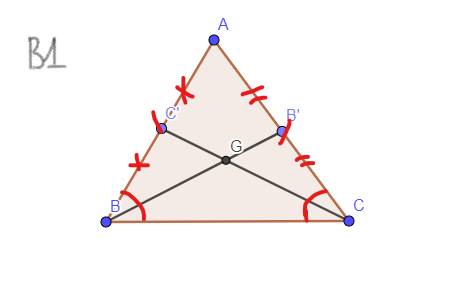
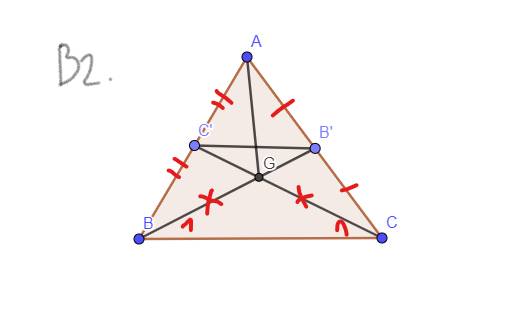
a: ΔABC cân tại A có BM,CN là các trung tuyến
Xét ΔABM và ΔACN có
AB=AC
góc A chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
b: Gọi G là giao của BM và CN
=>G là trọng tâm của ΔABC
=>GB=2/3BM; GC=2/3CN
mà BM=CN
nên GB=GC
=>góc GBC=góc GCB
Xét ΔNBC và ΔMCB có
NC=MB
BC chung
góc NCB=góc MBC
=>ΔNBC=ΔMCB
=>góc ABC=góc ACB
=>ΔBAC cân tại A


