Gọi AD và A'D' lần lượt là phân giác của tam giác ABC tại góc BAC và tam giác A'B'C' tại góc B'A'C'
tam giác ABC ~ tam giác A'B'C' => góc BAC = góc B'A'C'
=> góc BAD = 1/2 góc BAC = 1/2 góc B'A'C' = góc B'A'D' (AD và A'D' là phân giác)
Xét tam giác ABD và tam giác A'B'D' có :
1. góc ABD = góc A'B'D' ( do tam giác ABC ~ tam giác A'B'C' )
2. góc BAD = góc B'A'D' ( cmt )
Vậy tam giác ABD ~ tam giác A'B'D' (g-g)
=> AD/A'D' = AB/A'B' = k
CMTT cho phân giác 2 góc còn lại ta cũng có điều cần chứng minh.
Bài 7: Trường hợp đồng dạng thứ ba
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k ?
Chứng minh rằng, nếu hai tam giác ABC và A'B'C' đồng dạng với nhau thì :
a) Tỉ số của hai đường phân giác tương ứng bằng tỉ số đồng dạng
b) Tỉ số của hai trung tuyến tương ứng bằng tỉ số đồng dạng
Tam giác vuông ABC có widehat{A}90^0 và đường cao AH. Từ điểm H hạ đường HK vuông góc với AC (h.27)
a) Hỏi trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau ?
b) Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng ?
Đọc tiếp
Tam giác vuông ABC có \(\widehat{A}=90^0\) và đường cao AH. Từ điểm H hạ đường HK vuông góc với AC (h.27)
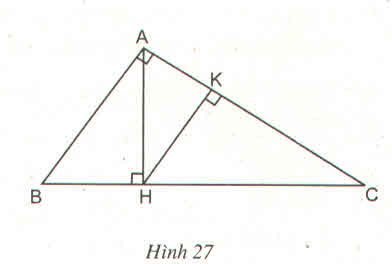
a) Hỏi trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau ?
b) Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng ?
Cho tam giác ABC vuông tại C (ACBC). Vẽ tia phân giác Ax của BAC cắt cạnh BC tại I. Vẽ BH vuông góc tại Ax tại H.a) Chứng minh tam giác AIC đồng dạng tam giác ABHb) Chứng minh HB 2 HI.HAc) Kẻ đường cao CK của tam giác ABC Kẻ KD là đường phân giác của tam giác CKA. Chứng minh dfrac{CD}{DA}dfrac{CB}{CA} Xin hãy giúp mình với ạ! Mình xin cám ơn!
Đọc tiếp
Cho tam giác ABC vuông tại C (AC<BC). Vẽ tia phân giác Ax của BAC cắt cạnh BC tại I. Vẽ BH vuông góc tại Ax tại H.
a) Chứng minh tam giác AIC đồng dạng tam giác ABH
b) Chứng minh HB 2 = HI.HA
c) Kẻ đường cao CK của tam giác ABC> Kẻ KD là đường phân giác của tam giác CKA. Chứng minh \(\dfrac{CD}{DA}=\dfrac{CB}{CA}\)
Xin hãy giúp mình với ạ! Mình xin cám ơn!
Cho tam giác ABC vuông góc tại A, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. a, Chứng minh AH = MN b, Chứng minh tam giác AHM đồng dạng với tam giác AHB rồi suy ra AH^2 = AM . AB c, Chứng minh tam giác AMN đồng dạng với tam giác ACB d, Cho AB = 6cm, AC = 8cm. Tính diện tích của tam giác AMN.
Cho tam giác ABC vuông tại A, AB=6cm,AC=8cm, đường cao AH (H thuộc BC)
a) Tính BC
b) Chứng minh rằng tam giác AHB đồng dạng tam giác CHA
c) Gọi BD là đường phân giác của góc B ( D thuộc AC). Tính DA,DC
Giải giúp em gấp ạ! Cảm ơn
cho tam giác nhọn ABC có các đường cao AD, BE và CF đồng quy tại H. Chứng minh:
a, tam giác AEF đồng dạng với tam giác ABC
b, H là giao điểm các đường phân giác của tam giác DEF
c, BH.BE + CH.CF = BC2
cho tam giác ABC vuông tại A có AB=6cm ,AC=8cm. đường cao AH và phân giác BDcắt nhau tại I (H trên BC và D trên AC)
a)tính độ dài AD,DC
b)Chướng minh tam giác ABC đồng dạng tam giác HBA và AB2=BH.BC
c)chứng minh tam giác ABI đồng dang với tam giác CBD
Cho hình thang MNPQ (MN//PQ, MN<PQ). Gọi E là giao điểm của MQ và NP. Đường phân giác trong của góc E cắt MN, PQ lần lượt tại D, K.
a) Chứng minh hai tam giác EDM và EKQ đồng dạng.
b) Chứng minh: EM.EK=EQ.ED
Giúp em với ạ
