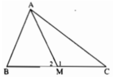
- Nếu A, B, C không thẳng hàng thì 3 điểm A, B, C tạo thành 3 đỉnh của 1 tam giác.
Trong tam giác ABC ta có AB + AC > BC
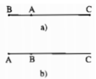
- Nếu A, B, C thẳng hàng và A ở giữa B và C hoặc trùng B, C thì AB + AC = BC
• Nếu A nằm giữa B và C thì AB + AC = BC.
• Nếu B nằm giữa A và C thì AB + BC = AC nên AC > BC.
Suy ra: AC + AB > BC
• Nếu C nằm giữa A và B thì AC + CB = AB nên AB > BC.
Suy ra: AB + AC > BC.
Vậy với ba điểm A, B, C bất kỳ ta luôn có AB + AC ≥ BC