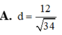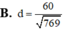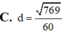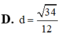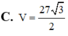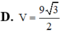Các câu hỏi tương tự
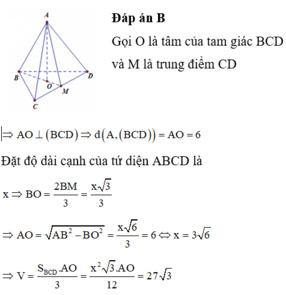
Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD A.
V
27
3
B.
V
5
3
C.
V
27
3
2
D.
V...
Đọc tiếp
Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD
A. V = 27 3
B. V = 5 3
C. V = 27 3 2
D. V = 9 3 2
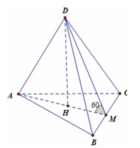
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng
60
O
. Tính thể tích V của khối tứ diện ABCD theo a:
Đọc tiếp
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 O . Tính thể tích V của khối tứ diện ABCD theo a:
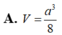
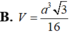
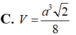
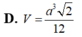
Cho tứ diện ABCD có ABAD
a
2
, BCBDa, CACDx. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a
3
3
12
. Góc giữa hai mặt phẳng (ACD) và (BCD) là A.
60
o...
Đọc tiếp
Cho tứ diện ABCD có AB=AD= a 2 , BC=BD=a, CA=CD=x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 o
B. 45 o
C. 90 o
D. 120 o
Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ đỉnh B đến mặt phẳng (ACD).
A
.
a
6
2
B
.
a
3
2
C
.
a
6
3
D
....
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ đỉnh B đến mặt phẳng (ACD).
A . a 6 2
B . a 3 2
C . a 6 3
D . a 2 3
Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là:
Đọc tiếp
Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là:
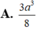
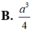
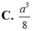
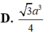
Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB3 cm, BC4 cm,
A
D
6
c
m
, AC5 cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng A.
12
5
cm
B.
12
7
cm
C.
6
cm
D.
6
10
cm
Đọc tiếp
Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB=3 cm, BC=4 cm, A D = 6 c m , AC=5 cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng
A. 12 5 cm
B. 12 7 cm
C. 6 cm
D. 6 10 cm
Cho tứ diện ABCD có BD 3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là A.
a
r
c
sin
33
40
B.
a
r
c...
Đọc tiếp
Cho tứ diện ABCD có BD =3, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 11, số đo góc giữa hai mặt phẳng (ABD) và (BCD) là
A. a r c sin 33 40
B. a r c sin 11 40
C. a r c cos 33 40
D. a r c cos 11 40
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích
a
3
3
6
Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy A.
d
a
3
4
B. ...
Đọc tiếp
Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), ACAD4,AB3, BC5 Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).
Đọc tiếp
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC=AD=4,AB=3, BC=5 Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).