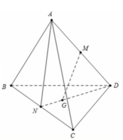
a: Xét ΔCBD có M,N lần lượt là trung điểm của CD,CB
=>MN là đường trung bình của ΔCBD
=>MN//BD
mà \(BD\subset\left(ABD\right)\) và MN không nằm trong mp(ABD)
nên MN//(ABD)
b: Chọn mp(ACD) có chứa AM
\(CD\subset\left(ACD\right);CD\subset\left(BCD\right)\)
Do đó: \(\left(ACD\right)\cap\left(BCD\right)=CD\)
Ta có: \(M=AM\cap CD\)
=>M là giao điểm của AM với mp(BCD)
=>AM cắt mp(BCD) tại M
c: \(N\in BC\subset\left(ABC\right);A\in\left(ABC\right)\)
Do đó: \(AN\subset\left(ABC\right)\)