Question

Cho tứ diện ABCD. Gọi E là trung điểm của AB và F là trung điểm thuộc cạnh AC sao cho EF không song song với BC. Tìm giao tuyến của các mặt phẳng sau:

a) (CDE) và (ABD)

b) (DEF) và (ABC)

Answer 1

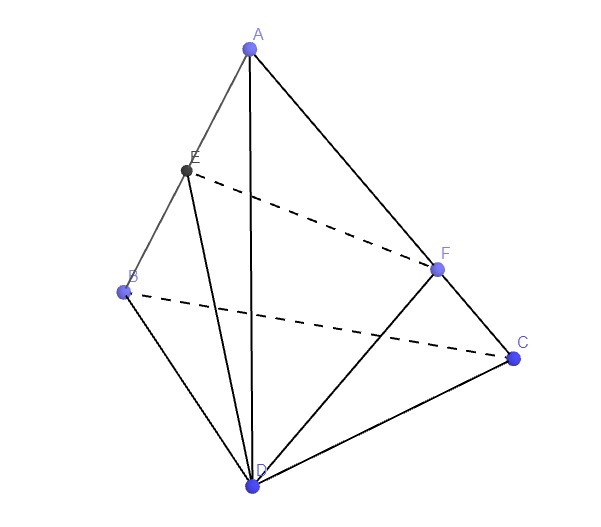
a.

\(\left\{{}\begin{matrix}D\in\left(CDE\right)\\D\in\left(ABD\right)\end{matrix}\right.\) \(\Rightarrow D\in\left(CDE\right)\cap\left(ABD\right)\)

\(\left\{{}\begin{matrix}E\in\left(CDE\right)\\E\in AB\in\left(ABD\right)\end{matrix}\right.\) \(\Rightarrow E\in\left(CDE\right)\cap\left(ABD\right)\)

\(\Rightarrow DE=\left(CDE\right)\cap\left(ABD\right)\)

b.

\(\left\{{}\begin{matrix}E\in\left(DEF\right)\\E\in AB\in\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow E\in\left(DEF\right)\cap\left(ABC\right)\)

\(\left\{{}\begin{matrix}F\in\left(DEF\right)\\F\in AC\in\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow F\in\left(DEF\right)\cap\left(ABC\right)\)

\(\Rightarrow EF=\left(DEF\right)\cap\left(ABC\right)\)

Answer 2