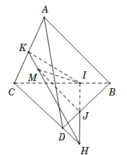
Trong mặt phẳng (BCD); IJ cắt CD tại H nên H thuộc (ACD)
Điểm H thuộc IJ m suy ra bốn điểm M; I; J; H đồng phẳng.
Nên trong mặt phẳng (IJM) , MH cắt IJ tại H và M H ⊂ I J M .
Mặt khác M ∈ A C D H ∈ A C D ⇒ M H ⊂ A C D .
Vậy giao tuyến của 2 mặt phẳng (ACD) và ( IJM) là MH
Chọn D.

