Các câu hỏi tương tự
Cho hình lăng trụ
A
B
C
.
A
B
C
có đáy ABC là tam giác đều cạnh a, tam giác A BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC. Tính cosin góc
α
giữa hai đường thẳng AA và BM. A.
cos
α
2
22
11
B.
cos
α...
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho tam giác ABC có AC=6cm,AB=8cm.Trên cạnh AB lấy điểm M sao cho BM=3cm,từ M kẻ MN vuông góc với BC.Gọi D là giao điểm của AC và MN.
a)Tính BC,MN,Snbm/Sabc
b)DA.DC+BN.BC=BD^2
P/s:Vẽ gíup mk cái hình nka
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc
α
là góc giữa hai đường thẳng AA’ và BM A.
cos
α
2
22
11
B.
cos
α
11
11
C.
cos...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc α là góc giữa hai đường thẳng AA’ và BM
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, AB4cm Tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABC) .M thuộc SC sao cho
C
M
2
M
S
. Khoảng cách giữa hai đường
A
C
v
à
B
M
là ? A.
4
21
21
c
m
B....
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, AB=4cm Tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABC) .M thuộc SC sao cho C M = 2 M S . Khoảng cách giữa hai đường A C v à B M là ?
A. 4 21 21 c m
B. 8 21 21 c m
C. 2 21 3 c m
D. 4 21 7 c m
Cho hình hộp ABCD.ABCD, AB6cm, BCBB2cm. Điểm E là trung điểm cạnh BC. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng C E′, hai đỉnh P, Q nằm trên đường thẳng đi qua điểm B′ và cắt đường thẳng AD tại điểm F. Khoảng cách DF bằng A. 1cm B. 2cm C. 3cm D. 6cm
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D', AB=6cm, BC=BB'=2cm. Điểm E là trung điểm cạnh BC. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng C E′, hai đỉnh P, Q nằm trên đường thẳng đi qua điểm B′ và cắt đường thẳng AD tại điểm F. Khoảng cách DF bằng
A. 1cm
B. 2cm
C. 3cm
D. 6cm
Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều ABC có cạnh bằng 90(cm). Bạn muốn cắt mảnh tôn hình chữ nhật MNPQ từ mảnh tôn nguyên liệu (với M, N thuộc cạnh BC, P và Q tương ứng thuộc cạnh AC và AB) để tạo thành hình trụ có chiều cao bằng MQ. Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là A.
91125
4
π
c...
Đọc tiếp
Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều ABC có cạnh bằng 90(cm). Bạn muốn cắt mảnh tôn hình chữ nhật MNPQ từ mảnh tôn nguyên liệu (với M, N thuộc cạnh BC, P và Q tương ứng thuộc cạnh AC và AB) để tạo thành hình trụ có chiều cao bằng MQ. Thể tích lớn nhất của chiếc thùng mà bạn A có thể làm được là
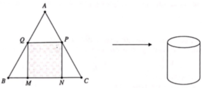
A. 91125 4 π c m 3
B. 91125 2 π c m 3
C. 13500 3 π c m 3
D. 108000 π c m 3
cho hình chữ nhật ABCD có diện tích 120cm2 . kéo dài cạnh AB, BC, CD, DA một đoạn sao cho BM=AB , CN=BC , DH=CD , AK=AD. nối MNHK. tìm diện tích tứ giác MNHK
Cho hình chóp S.ABC có
S
A
S
B
S
C
3
,
tam giác ABC vuông cân tại B và
A
C
2
2
. Gọi M, N lần lượt là trung điểm của AC và BC. Trên hai cạnh SA, SB lấy các điểm P, Q tương ứng sao cho
S
P
1
,
S
Q
2.
Tính thể tích V của khối tứ diện...
Đọc tiếp
Cho hình chóp S.ABC có S A = S B = S C = 3 , tam giác ABC vuông cân tại B và
A C = 2 2 . Gọi M, N lần lượt là trung điểm của AC và BC. Trên hai cạnh SA, SB lấy các điểm P, Q tương ứng sao cho S P = 1 , S Q = 2. Tính thể tích V của khối tứ diện M N P Q .
A. V = 7 18
B. V = 3 12
C. V = 34 12
D. V = 34 144
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0xa). Mặt phẳng
(
α
)
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.
x
a
4
B.
x
a
3
C.
x
a...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0<x<a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5

