Ta có: S△HCN=S△KAM
S△KDH=S△NBM
Mà ta có:SMNHK=S△HCN+S△KAM+ S△KDH+S△NBM+SABCD=2S△HCN+2S△KDH+SABCD
=HC.CN+KD.DH+120=2DC.BC+2AD.DC+120=2DC(BC+AD)+120=2DC.2BC+120=4DC.BC+120=4.120+120=5.120=600 (cm2)
Vậy SMNHK=600 cm2
Ta có: S△HCN=S△KAM
S△KDH=S△NBM
Mà ta có:SMNHK=S△HCN+S△KAM+ S△KDH+S△NBM+SABCD=2S△HCN+2S△KDH+SABCD
=HC.CN+KD.DH+120=2DC.BC+2AD.DC+120=2DC(BC+AD)+120=2DC.2BC+120=4DC.BC+120=4.120+120=5.120=600 (cm2)
Vậy SMNHK=600 cm2
Cho hình chữ nhất ABCD có cạnh AB = 6, AD = 4. Gọi M, N, P, Q lần lượt là trung điểm bốn cạnh AB, BC, CD, DA. Cho hình chữ nhất ABCD quay quanh QN, khi đó tứ giác MNPQ tạo thành vật tròn xoay có thể tích bằng
A . 4 π
B . 8 π
C . 10 π
D . 24 π
Cho tứ diện ABCD có thể tích bằng 3. Gọi N, P lần lượt là trung điểm của BC, CD; M là điểm đoạn AB sao cho B M = 2 A M . Mặt phẳng (MNP) cắt AD tại Q. Thể tích khối đa diện AMQPCN bằng
A. 7 3
B. 15 16
C. 7 6
D. 15 8
Cho tứ diện ABCD có các cạnh A D = B C = 3 , A C = B D = 4 ; A B = C D = 2 3 . Thể tích tứ diện ABCD bằng:
A. 2740 12
B. 2047 12
C. 2074 12
D. 2470 12
Có một mảnh bìa hình chữ nhật ABCD với AB=4a, AD=2a. Người ta đánh dấu M là trung điểm của AB, N và P là các điểm thuộc CD sao cho DN = CP = a. Sau đó người ta cuốn mảnh bìa lại sao cho cạnh BC trùng với cạnh AD tạo thành một hình trụ. Tính thể tích của tứ diện AMNP với các đỉnh A, M, N, P nằm trên hình trụ vừa tạo thành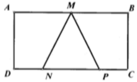
![]()
![]()
![]()
Cho tứ diện ABCD có AB vuông góc với CD, AB=CD=6. M là điểm thuộc canh BC sao cho MC=x.BC (0<x<1). Mặt phẳng (P) đi qua M và song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Diện tích lớn nhất S m a x của tứ giác MNPQ bằng bao nhiêu?
A. 9
B. 4,5
C. 36
D. 18
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau AB=3, AC=4, AD=5. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Tính thể tích tứ diện AMNP
A. 5 2
B. 8 3
C. 20 7
D. 15 6
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau A B = 3 , A C = 4 , A D = 5 . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Tính thể tích tứ diện AMNP.
A. 15 6
B. 20 7
C. 8 3
D. 5 2
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, A B = 6 a , A C = 7 a , A D = 8 a . . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
A. 14 a 2
B. 28 a 2
C. 42 a 2
D. 7 a 2
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, A B = 6 a , A C = 5 a , A D = 4 a . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
A. V = 5 a 3 3 .
B. V = 20 a 3 3 .
C. V = 5 a 3
D. V = 10 a 3