Đáp án C
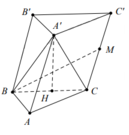
Ta có cos α = cos C C ' ; B M ^ = cos B M C ^ .
Cạnh A ' H = B C 3 2 = a 3 2 , A H = A B 3 2 = a 3 2
A A ' = A ' H 2 + A H 2 = a 6 2 ⇒ M C = a 6 4 .
Cạnh B ' H = A ' B ' 2 + A ' H 2 = a 7 2 .
Do đó cos B ' B H ^ = B B ' 2 + B H 2 - B ' H 2 2 B B ' . B H = 0 ⇒ B ' B ⊥ B H
⇒ M C ⊥ B C ⇒ c o s M B C ^ = M C B M = M C B C 2 + M C 2 = 33 11 .

