b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)
Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE
Vậy BD là đường trung trực của AE (0.5 điểm)

b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)
Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE
Vậy BD là đường trung trực của AE (0.5 điểm)
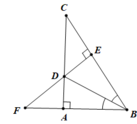
Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng: BD là đường thẳng trung trực của AE
cho tam giác abc vuông tại a. tia phân giác góc b cắt ac tại d kẻ DE vuông góc với BC tại E.
a) tam giác ABD=tam giác EBD.
b)BD là đường trung trực của AE
c)gọi F là giao điểm của đoạn thẳng ED và AB . Chứng minh : AE//CF và AD<CD
Cho tam giác ABC vuông tại A có BD là đường phân giác của góc B. Kẻ DE BC (E BC). Gọi F là giao điểm của tia BA và tia ED. Chứng minh: a/ ABD = EBD. Từ đó suy ra BD là đường trung trực của AE. b/ AD < DC. c/ AE // FC.
Cho △ ABC vuông tại A ,tia phân giác của góc B cắt AC tại D kẻ DE vuông góc BC (E ∈ BC). Chứng minh △ BAD = △ BED
Cho △ ABC vuông tại A ,tia phân giác của góc B cắt AC tại D kẻ DE vuông góc BC (E ∈BC)
a) Chứng minh △BAD=△BED
b) Chứng minh BD là đường trung trực của đoạn thẳng AE
c) Gọi F là giao điểm của hai đường thẳng AB và DE . Chứng minh AE // FC
Cho tam giác ABC vuông tại a có tia phân giác của góc ABC cắt AC tại d trên cạnh BC lấy điểm e sao cho be = ba a c/m tam giác bad bằng tam giác bed và BD là đường trung trực của đoạn AE b gọi f là giao điểm của hai đường thẳng de và da chứng minh AF = AC câu c chứng minh AE song song với SC câu d gọi I là trung điểm của SC chứng minh ba điểm b d I thẳng hàng
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
d. AD < DC
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a. ∆ABD = ∆EBD
Cho tam giác ABC vuông tại A. Kẻ đường phân giác BD, kẻ DE vuông góc với BC (E thuộc BC). a) Chứng minh rằng: BD là trung trực của AE và AD < DC. b) Tia ED cắt tia BA tại F. Chứng minh: BD vuông góc với CF và AE // CF.c) Tia BD cắt FC tại G. Chứng minh rằng D cách đều ba cạnh của tam giác AEG. d) Lấy M và N tương ứng di động trên BF và BC sao cho BM + BN = BC. Chứng minh rằng trung điểm I của MN luôn nằm trên một đường thẳng cố định.
Chỉ cần làm phần c,d
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
c. DF = DC