Question

Cho tam giác ABC vuông tại A. M thuộc BC. Gọi H là hình chiếu của M trên AB, K là hình chiếu của M trên AC

a) C/m: AM=HK

b) M ở vị trí nào trên BC thì AM vuông góc HK?

c) M ở vị trí nào trên BC thì HK nhỏ nhất?

Answer 1

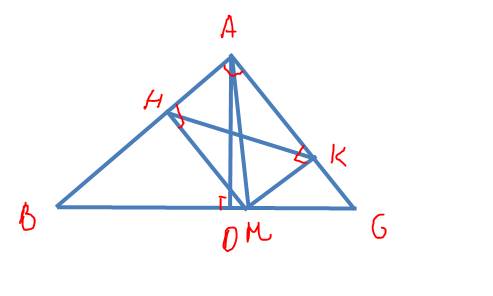
a) Xét tứ giác AHMK có:

\(\widehat{A}=\widehat{H}=\widehat{K}=90^{ }\) độ

\(\Rightarrow AHMK\) là hình chữ nhật ( theo dấu hiệu nhận biết )

\(\Rightarrow AM=HK\)

b) Nếu \(AM\perp HK\Rightarrow AHMK\) là hình vuông ( theo dấu hiệu nhận biết)

\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) = 90 độ

\(\Rightarrow AM\) là tia phân giác của \(\widehat{BAC}\) thì \(AM\perp HK\)

c) Vì \(AM=HK\Rightarrow\) HK nhỏ nhất \(\Leftrightarrow\) AM nhỏ nhất.

Kẻ \(AD\perp BC\) ( D cố định )

\(\Rightarrow\Delta AMD\) vuông tại D

\(\Rightarrow AM\ge AD\)

 Nếu \(AM=AD\Rightarrow AM\perp BC\)

Vậy nếu để HK nhỏ nhất thì M phải trùng D