Question

Cho tam giác ABC vuông tại A, đường trung tuyến AM. Từ M vẽ ME 1 AB, MF 1 AC (E∈ AB, F∈ AC). a) Chứng minh tứ giác AEMF là hình chữ nhật. b) Gọi H đối xứng với M qua E.Gọi G đối xứng với M qua F. Chứng minh H, A, G

Giải giùm em câu b vs ạ:(

Answer 1

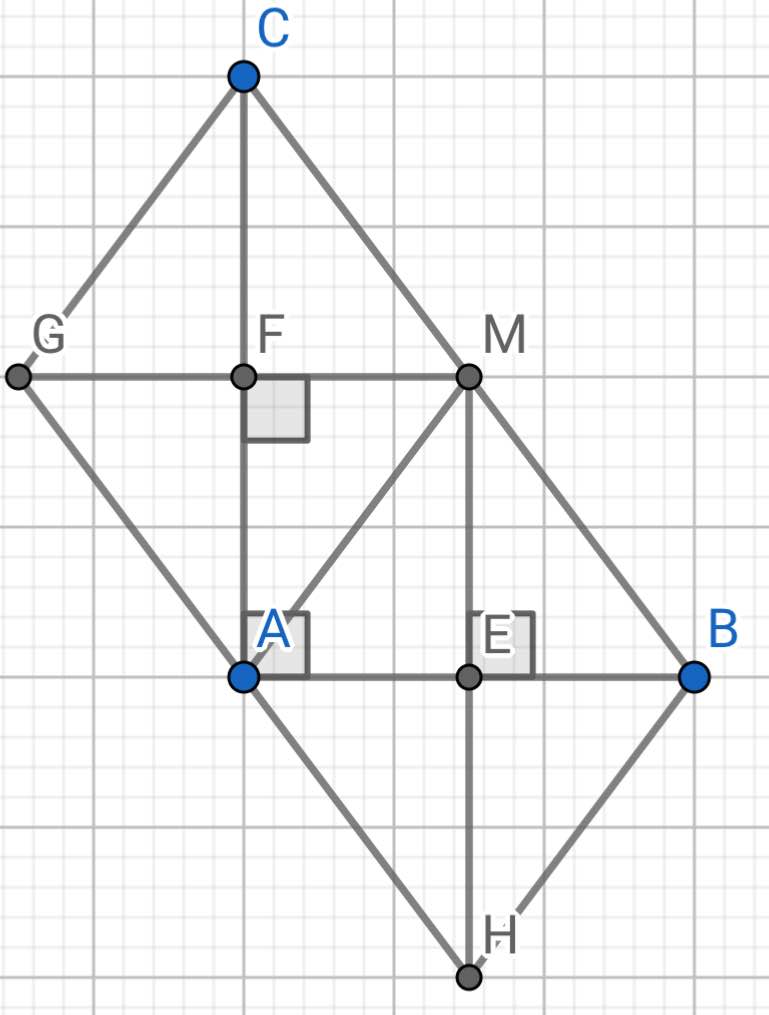
a) Do ME ⊥ AB (gt)

=> ∠AEM = 90⁰

MF ⊥ AC (gt)

=> ∠AFM = 90⁰

ΔABC vuông tại A (gt)

=> ∠BAC = 90⁰

=> ∠EAF = 90⁰

Tứ giác AEMF có:

∠AFM = ∠AEM = ∠EAF = 90⁰

=> AEMF là hình chữ nhật

b) Do AM là đường trung tuyến của ΔABC (gt)

=> M là trung điểm BC

Mà ME ⊥ AB (gt)

=> ME // AC

=> E là trung điểm của AB

Do M đối xứng với H qua E (gt)

=> E là trung điểm của MH

Tứ giác AMBH có:

E là trung điểm của AB (cmt)

E là trung điểm của MH (cmt)

=> AMBH là hình bình hành

=> AH // BM

=> AH // BC    (1)

Do MF ⊥ AC

=> MF // AB

Mà M là trung điểm của BC (cmt)

=> F là trung điểm của AC

Do M và G đối xứng qua F (gt)

=> F là trung điểm của MG

Tứ giác AMCG có:

F là trung điểm của AC (cmt)

F là trung điểm của MG (cmt)

=> AMCG là hình bình hành

=> AG // MC

=> AG // BC    (2)

Từ (1), (2) và tiên đề Euclide suy ra H, A, G thẳng hàng

Answer 2

Giúp với ạ mai em thi r:v

Answer 3

Dạ em cảm ơn ạ