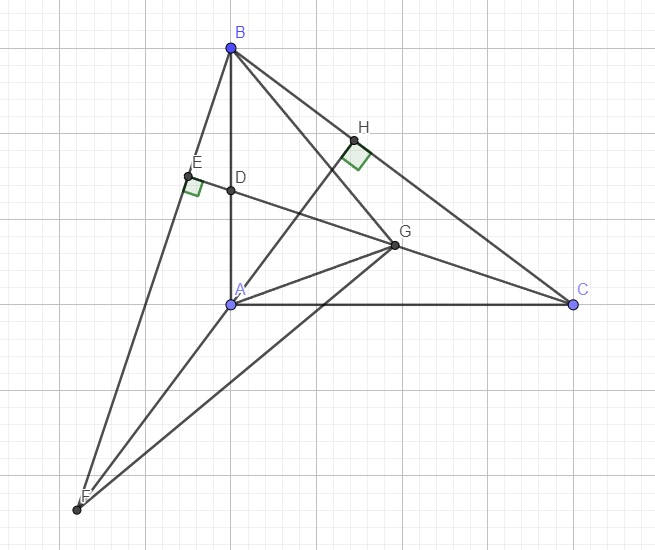
cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC) biết AB = 18cm, AC = 24cm
a) Chứng minh AB2 = BH x BC
b) Kẻ đường phân giác CD của tam giác ABC (D thuộc AB). Tính độ dài DA
c) Từ B kẻ đường thẳng vuông góc với CD tại E và cắt đường thẳng AH tại F. Trên CD lấy G sao cho BA = BG. Chứng minh BG vuông góc với FG
Chắc em cần câu c thôi, 2 câu còn lại khá đơn giản:
Xét 2 tam giác vuông BEC và BHF có: \(\left\{{}\begin{matrix}\widehat{B}-chung\\\widehat{BEC}=\widehat{BHF}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta BEC\sim\Delta BHF\left(g.g\right)\Rightarrow\dfrac{BE}{BH}=\dfrac{BC}{BF}\Rightarrow BH.BC=BE.BF\)
Kết hợp câu a \(\Rightarrow AB^2=BE.BF\)
Lại có \(BA=BG\Rightarrow BG^2=BE.BF\Rightarrow\dfrac{BG}{BE}=\dfrac{BF}{BG}\)
Xét 2 tam giác BGF và BEG có:
\(\left\{{}\begin{matrix}\widehat{GBF}-chung\\\dfrac{BG}{BE}=\dfrac{BF}{BG}\end{matrix}\right.\) \(\Rightarrow\Delta BGF\sim\Delta BEG\left(c.g.c\right)\)
\(\Rightarrow\widehat{BGF}=\widehat{BEG}=90^0\)
\(\Rightarrow BG\perp FG\)