a: Xét tứ giác EAFH có
\(\widehat{EAF}=\widehat{AEH}=\widehat{AFH}=90^0\)
Do đó: EAFH là hình chữ nhật
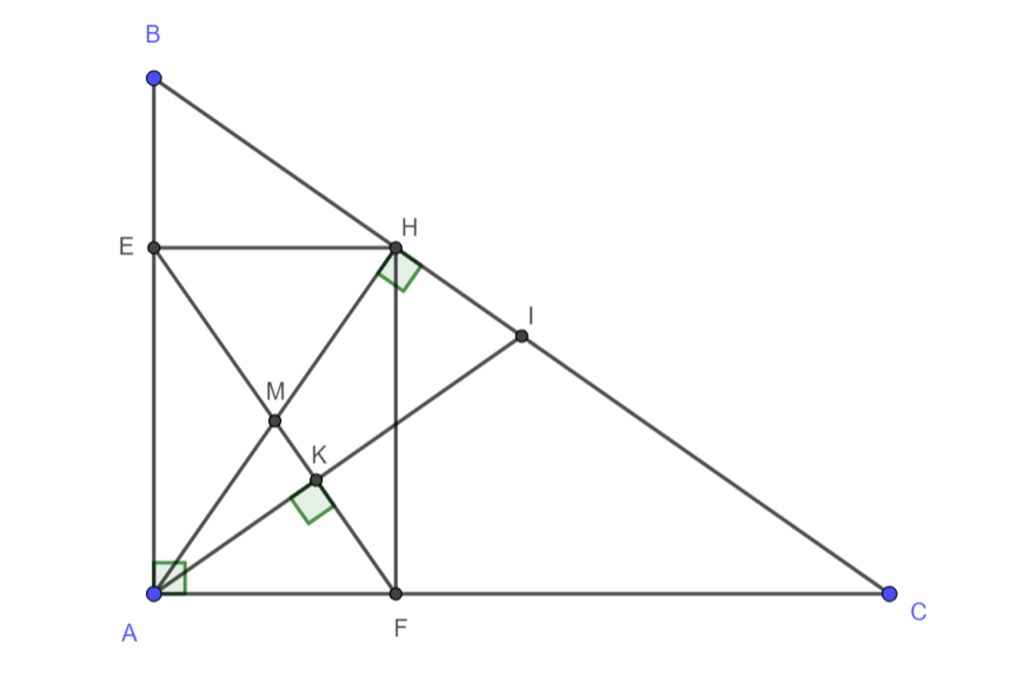
a) Xét tứ giác AEHF có:
∠A = ∠E = ∠F= 90o
⇒ AEHF là hình chữ nhật (dấu hiệu nhận biết)
b) Gọi M = AH∩EF
K = AI∩EF
Vì ∠K = ∠H = 90o
∠A chung
⇒ ΔAKM và ΔAHI đồng dạng (g.g)
⇒ ∠AMK = ∠AIH (hai góc tương ứng)
Vì tứ giác AEHF là hình chữ nhật (cmt)
⇒ Giao điểm của hai đường chéo là trung điểm của mỗi đường và hai đường chéo bằng nhau
⇒




