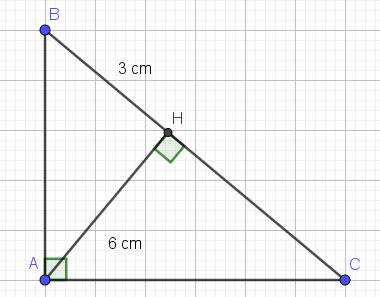
ΔAHB vuông tại H
=>AB^2=AH^2+HB^2
=>AB=3*căn 5(cm)
ΔAHB vuông tại H có sin B=AH/AB=6/3*căn 5=2/căn 5
Lời giải:
Áp dụng định lý Pitago:
$AB=\sqrt{BH^2+AH^2}=\sqrt{6^2+3^2}=3\sqrt{5}$ (cm)
Xét tam giác vuông $ABH$ vuông tại $H$ ta có:
$\sin B =\frac{AH}{AB}=\frac{6}{3\sqrt{5}}=\frac{2}{\sqrt{5}}$