Lời giải:
a.
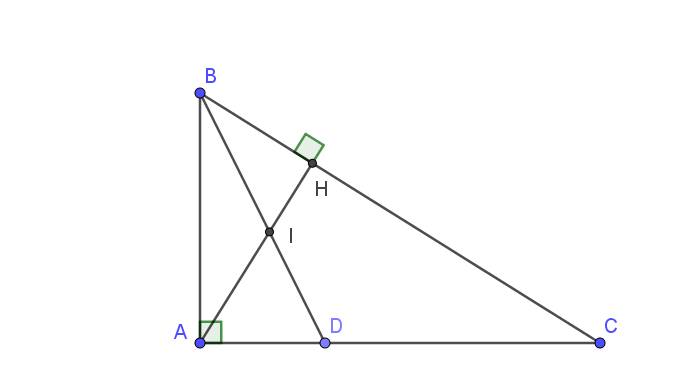
Xét tam giác $ABC$ và $HBA$ có:
$\widehat{B}$ chung
$\widehat{BAC}=\widehat{BHA}=90^0$
$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)
$\Rightarrow \frac{AB}{HB}=\frac{AC}{HA}$
$\Rightarrow AB.HA=AC.HB$
b.
$BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25$ (cm) - áp dụng định lý Pitago
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{15.20}{25}=12$ (cm)
$HB=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
c.
Tam giác $ABH$ có $BI$ là phân giác. Áp dụng tính chất tia phân giác:
$\frac{IH}{IA}=\frac{BH}{BA}(1)$
Tam giác $ABC$ có $BD$ là phân giác. Áp dụng tính chất tia phân giác:
$\frac{DA}{DC}=\frac{AB}{BC}(2)$
Từ tam giác đồng dạng phần a suy ra $\frac{HB}{AB}=\frac{BA}{BC}(3)$
Từ $(1); (2); (3)\Rightarrow \frac{IH}{IA}=\frac{DA}{DC}$