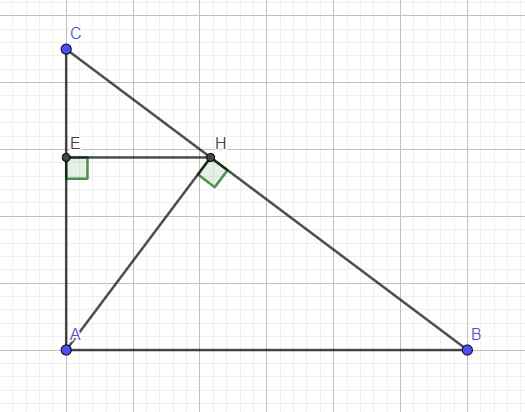
a: \(AH=\dfrac{9\cdot12}{15}=7.2\left(cm\right)\)
CH=5,4(cm)
Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=12\left(cm\right)\)
a.
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=7,2\left(cm\right)\)
\(AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=5,4\left(cm\right)\)
b.
Trong tam giác vuông ACH:
\(cosHAC=\dfrac{AH}{AC}\Rightarrow cos^2HAC=\dfrac{AH^2}{AC^2}\)
Áp dụng hệ thức lượng:
\(AH^2=AE.AC\Rightarrow AE=\dfrac{AH^2}{AC}=AC.\dfrac{AH^2}{AC^2}=AC.cos^2HAC\) (đpcm)