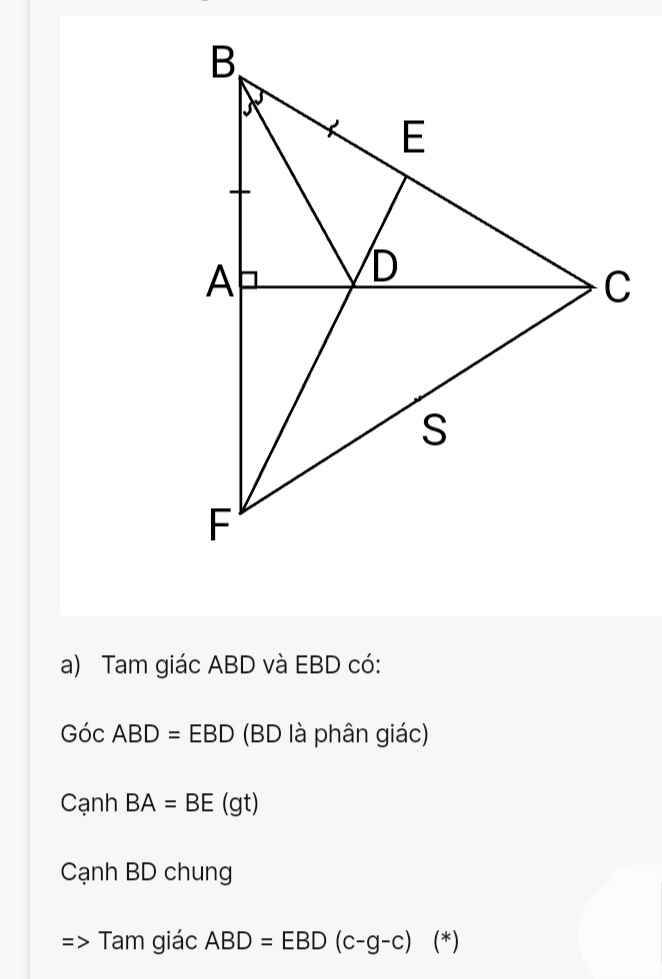
Cho tam giác ABC vuông tại A (AB<AC), kẻ BD là phân giác của góc ABC (D thuộc AC). Vẽ DE vuông góc với BC tại E. a) Chứng minh tam giác ABD = tam giác EBD. b) AE cắt BD tại I. Chứng minh BD vuông góc với AE và I là trung điểm AE. c) Cẽ tia Cx vuông góc với tia BD tại H. Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Chứng minh 3 điểm C,H,F thẳng hàng và AE // FC.
a) Ta có:
- Góc ABD là góc giữa hai phân giác của góc ABC, nên ABD = CBD.
- Góc EBD là góc giữa phân giác của góc ABC và đường thẳng DE, nên EBD = CBD.
Vậy tam giác ABD = tam giác EBD.
b) Ta có:
- Góc ABD = góc EBD (do chứng minh ở câu a).
- Góc ADB = góc EDB (do cùng là góc vuông).
- Vậy tam giác ABD = tam giác EBD (do hai góc bằng nhau và góc giữa hai cạnh bằng nhau).
- Do đó, BD vuông góc với AE.
- Ta có AE cắt BD tại I, vậy I là trung điểm của AE.
c) Ta có:
- Tia Cx vuông góc với tia BD tại H.
- Trên tia đối của tia AB, lấy điểm F sao cho AF = EC.
- Ta cần chứng minh 3 điểm C, H, F thẳng hàng và AE // FC.
- Vì AF = EC và tam giác ABD = tam giác EBD (do chứng minh ở câu a), nên tam giác AFB = tam giác EFC (do hai cạnh bằng nhau và góc giữa hai cạnh bằng nhau).
- Vậy 3 điểm C, H, F thẳng hàng và AE // FC.
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD vuông góc với AE tại trung điểm I của AE
c: Xét ΔBFC có \(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
nên AE//CF
Ta có: BD\(\perp\)AE
AE//CF
Do đó: BD\(\perp\)CF
mà BD\(\perp\)CH
và CH,CF có điểm chung là C
nên C,H,F thẳng hàng