a)xét tg ABD và tg CBD có:
+ AB=BE(gt)
+ góc ABD = EBD (BD là phân giác)
+BD chung
=>tg ABD= tg EBD(c.gc)
b) vì tg ABD=tgEBD
=> AD=DE và góc BAD = BED (=90 độ)
=> DE ⊥ BC
=> tg DEC có DC là cạnh huyền =>DC>ED mà ED=AD => DC>AD
c)xét tg BFE và tg BCA có:
+ Góc E = A (=90 độ)
+góc B chung
+ BE=BA
=>tg BFE =tg BCA (gcg)
=>BF=BC
=> tg BFC cân tại B
vì S là td FC
=>BS vừa là trung tuyến vừa là đường cao
=>BS⊥FC (1)
tg BFC có: D là giao của 2 đg cao CA và FE
=> D là trực tâm => BD ⊥ FC (2)
từ 1 và 2 => B,D,S thẳng hàng
Sửa đề: AB = BE (không phải AB = AE)
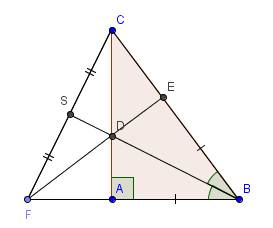
Gởi hình vẽ trước, đi công việc, tí sửa sau
Xét ∆ABD và ∆EBD có:
∠ABD = ∠EBD (do BD là phân giác của ∠B)
BD chung
AB = BE (gt)
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ ∠CED = 90⁰
⇒ ∆CED vuông tại E
⇒ CD là cạnh huyền nên là cạnh lớn nhất
⇒ CD > DE (1)
Do ∆ABD = ∆EBD (cmt)
⇒ AD = DE (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ CD > AD
c) Xét hai tam giác vuông:
∆ABC và ∆EBF có:
AB = BE (gt)
∠B chung
⇒ ∆ABC = ∆EBF (cạnh góc vuông - góc nhọn kề)
⇒ BC = BF (hai cạnh tương ứng)
⇒ ∆BCF cân tại B
Lại có BD là phân giác của ∠B
⇒ BD cũng là đường trung tuyến của ∆BCF
Mà S là trung điểm FC
⇒ B, D, S thẳng hàng


