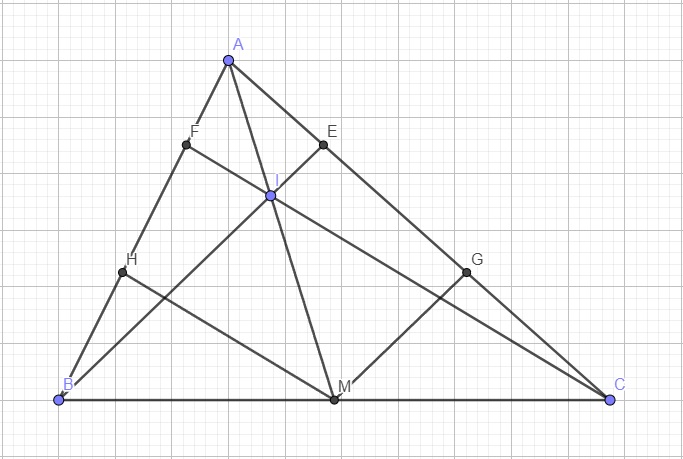
Qua M kẻ các đường thẳng song song BE và CF lần lượt cắt AC và AB tại G và H
Do M là trung điểm BC và \(MG||BE\Rightarrow MG\) là đường trung bình tam giác BCE
\(\Rightarrow G\) là trung điểm CE \(\Rightarrow GE=GC=\dfrac{1}{2}EC\)
Tương tự ta có H là trung điểm BF \(\Rightarrow BH=FH=\dfrac{1}{2}BF\)
Áp dụng định lý Talet trong tam giác AMG:
\(\dfrac{AE}{EG}=\dfrac{AI}{IM}\)
Áp dụng định lý Talet trong tam giác AMH:
\(\dfrac{AF}{FH}=\dfrac{AI}{IM}\)
\(\Rightarrow\dfrac{AE}{EG}=\dfrac{AF}{FH}\Rightarrow\dfrac{AE}{2EG}=\dfrac{AF}{2FH}\Rightarrow\dfrac{AE}{EC}=\dfrac{AF}{FB}\)
\(\Rightarrow EF||BC\) (định lý talet đảo)