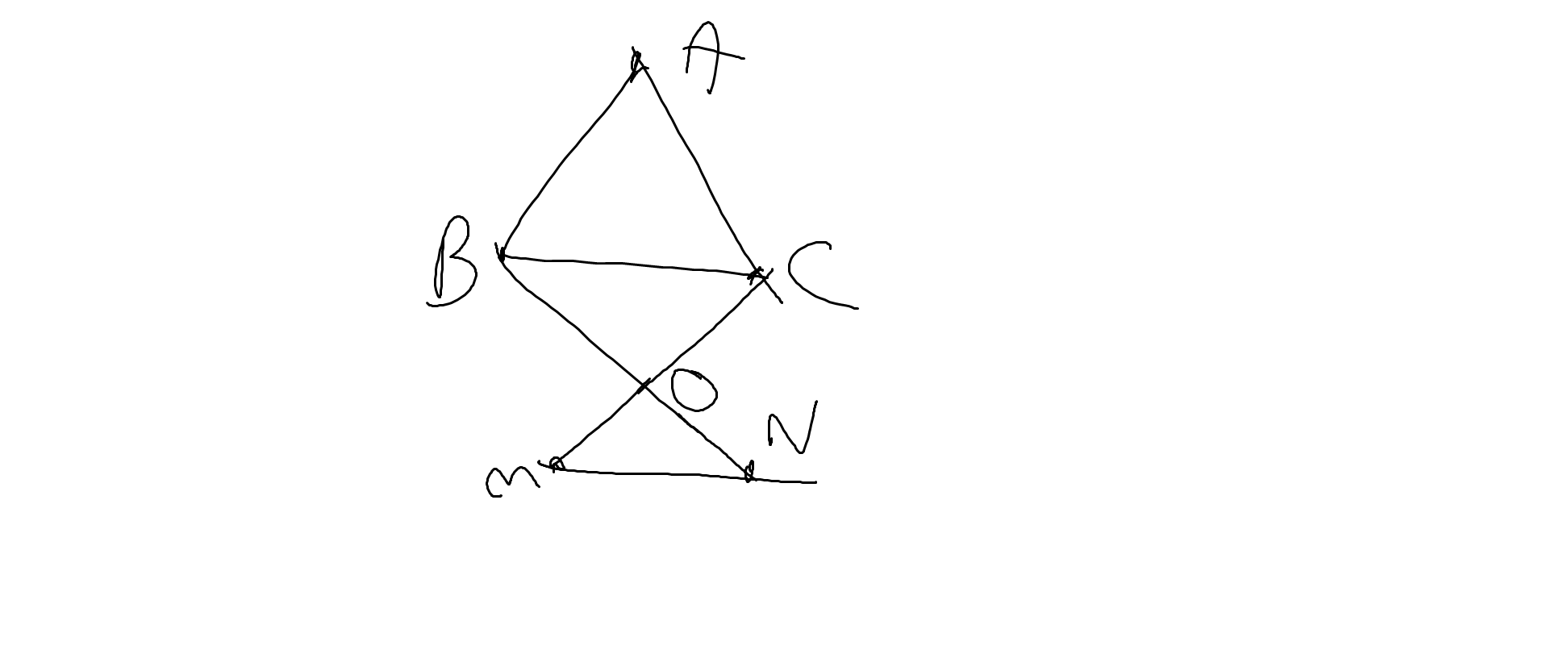
cho tam giác abc cân tại a. qua b kẻ đường thẳng vuông góc với ba, qua c kẻ đừog thẳng vuông góc với ca, hai đường thẳng này cắt nhau tại o. trên tia đối của tia oc lấy điểm m bất kỳ, qua m kẻ đường thẳng song song với bc cắt tia bo tại n. chứng minh tứ giác mbnc là hình thang cân
vẽ hình giúp em với ạ
Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
Xét ΔOBC và ΔONM có
\(\widehat{OBC}=\widehat{ONM}\)(hai góc so le trong, BC//MN)
\(\widehat{BOC}=\widehat{NOM}\)(hai góc đối đỉnh)
Do đó: ΔOBC~ΔONM
=>\(\dfrac{OB}{ON}=\dfrac{OC}{OM}\)
mà OB=OC
nên ON=OM
Ta có: ON+OB=NB
OM+OC=CM
mà ON=OM và OB=OC
nên NB=MC
Xét tứ giác BCNM có BC//MN
nên BCNM là hình thang
Hình thang BCNM có BN=CM
nên BCNM là hình thang cân