Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
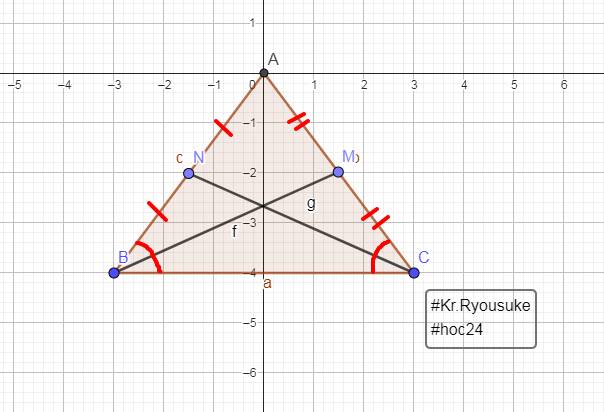
Mình xin phép sửa đề:
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABN = tam giác ACN , từ đó suy ra BM=CN
`------`
\(\text{GT | AB = AC, }\widehat{\text{B}}=\widehat{\text{C}}\)
\(\text{CM | BM = CN}\)
\(\text{BM là đường trung tuyến}\)
`->`\(\text{MA = MC (1)}\)
\(\text{CN là đường trung tuyến}\)
`->`\(\text{NA = NB (2)}\)
`\Delta ABC` cân tại A
`->`\(\widehat{\text{B}}=\widehat{\text{C}}\text{, AB = AC (3)}\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
`->`\(\text{NA = NB = MA = MC}\)
Xét `\Delta ABM` và `\Delta ACN`:
\(\left\{{}\begin{matrix}\text{BM = CN}\\\widehat{\text{B}}=\widehat{\text{C}}\\\text{BC chung}\end{matrix}\right.\)
`=> \Delta ABM = \Delta ACN (c-g-c)`
`->`\(\text{BM = CN (2 cạnh tương ứng).}\)