Mình xin phép sửa đề:
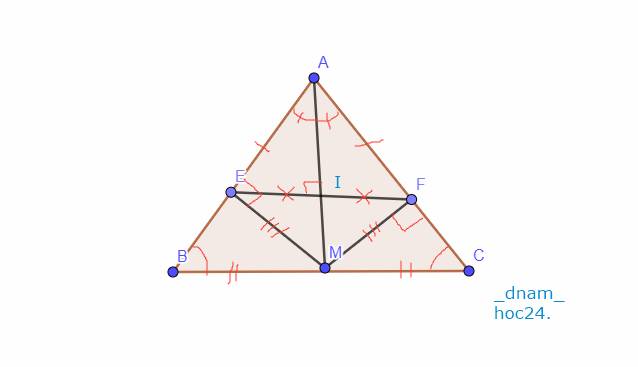
Cho tam giac ABC cân tại A, M là trung điểm của BC, ME vuông góc với AB, MF vuông góc với AC. Chứng minh ME = MF và AM là đường trung trực của EF.
\(\text {(1)}\)
Xét Tam giác `ABM` và Tam giác `ACM` có:
`AB = AC (\text {Tam giác ABC cân tại A})`
\(\widehat {B}= \widehat {C}(\text {Tam giác ABC cân tại A})\)
`MB = MC (\text {M là trung điểm của BC})`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`->`\(\widehat {BAM}=\widehat {CAM} (\text {2 góc tương ứng})\)
Xét Tam giác `AEM` và Tam giác `AFM` có:
`\text {AM chung}`
\(\widehat{BAM}=\widehat{CAM} (CMT)\)
\(\widehat{AEM}=\widehat{AFM} (=90^0)\)
`=> \text {Tam giác AEM = Tam giác AFM (ch-gn)}`
`-> ME = MF (2 cạnh tương ứng)`
\(\left(2\right)\)
Gọi `I` là giao điểm của `AM` và `EF`
C1:
Vì Tam giác `AEM =` Tam giác `AFM (\text {Theo CMT})`
`-> AE = AF (\text {2 cạnh tương ứng})`
Xét Tam giác `AEI` và Tam giác `AFI` có:
`AE = AF (CMT)`
\(\widehat{EAI}=\widehat{FAI} (\text {Theo CMT})\)
`\text {AI chung}`
`=> \text {Tam giác AEI = Tam giác AFI (c-g-c)}`
`-> IE = IF (\text {2 cạnh tương ứng})`
`->`\(\widehat{AIE}=\widehat{AIF} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{AIE}+\widehat{AIF}=180^0\)
`->`\(\widehat{AIE}=\widehat{AIF}=\)`180/2=90^0`
`-> \text {AI} \bot \text {EF}`
\(\text{Ta có: }\left\{{}\begin{matrix}\text{IE = IF }\\\text{AI}\perp\text{EF}\end{matrix}\right.\)
`-> \text {AI là đường trung trực của EF}`
`-> \text {AM là đường trung trực của EF}`
C2 (nếu bạn đã học về tính chất của tam giác cân với các đường Trung Tuyến, Đường Cao, Đường Trung Trực) :
Ta có:
AM vừa là đường phân giác, vừa là đường trung tuyến
`*` Theo tính chất của tam giác cân
`-> \text {AM là đường trung trực của EF (đpcm)}`
`@`\(\text{dnammv}\)