Question

Cho (O,R) cố định, dây AB ko đi qua tâm (O).Qua trung điểm I của dây AB,kẻ đường kính PQ vuông góc với AB (P thuộc cung nhỉ AB). E là điểm bất kì trên cung nhỉ QB (E ko trùng với B và Q),QE cắt AB tại M,PE cắt AB tại D

1,Chứng minh 4 điểm P,I,E,M cùng thuộc 1 đường tròn

2, Chứng minh PD.PE=PI.PQ=PB^2

Answer 1

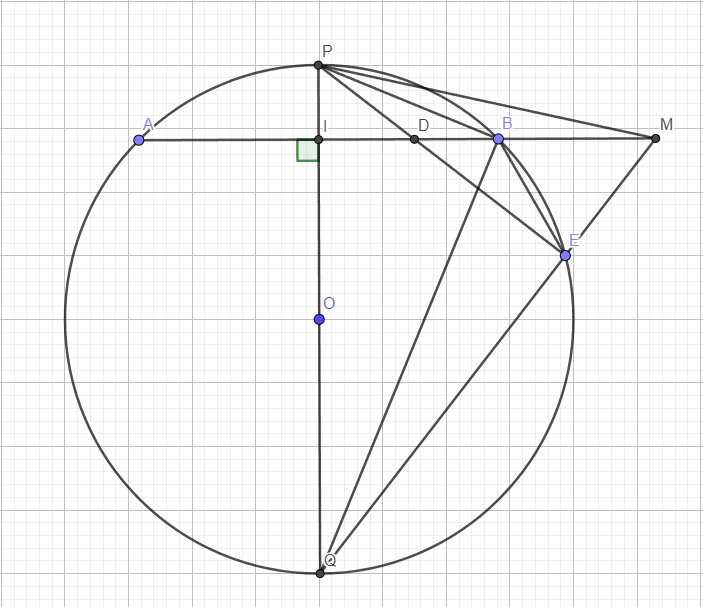
a. Em tự giải

b.

Do I là trung điểm AB \(\Rightarrow P\) là điểm chính giữa cung AB

\(\Rightarrow sđ\stackrel\frown{AP}=sđ\stackrel\frown{BP}\)

\(\Rightarrow\widehat{ABP}=\widehat{PEB}\) (2 góc nt chắn 2 cung bằng nhau)

Xét 2 tam giác PBD và PEB có:

\(\left\{{}\begin{matrix}\widehat{BPD}-chung\\\widehat{ABP}=\widehat{PEB}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta PBD\sim\Delta PEB\left(g.g\right)\)

\(\Rightarrow\dfrac{PB}{PE}=\dfrac{PD}{PB}\Rightarrow PD.PE=PB^2\)

I là trung điểm AB và PQ là đường kính qua I \(\Rightarrow PQ\perp AB\) tại I \(\Rightarrow\widehat{PIB}=90^0\)

PQ là đường kính \(\Rightarrow\widehat{PBQ}=90^0\) (góc nt chắn nửa đường tròn)

Xét 2 tam giác PIB và PBQ có:

\(\left\{{}\begin{matrix}\widehat{IPB}-chung\\\widehat{PIB}=\widehat{PBQ}=90^0\end{matrix}\right.\)

\(\Rightarrow\Delta PIB\sim\Delta PBQ\)

\(\Rightarrow\dfrac{PI}{PB}=\dfrac{PB}{PQ}\Rightarrow PI.PQ=PB^2\)

\(\Rightarrow PD.PE=PI.PQ=PB^2\)

Answer 2