Bài 8: Các trường hợp đồng dạng của tam giác vuông
Các câu hỏi tương tự
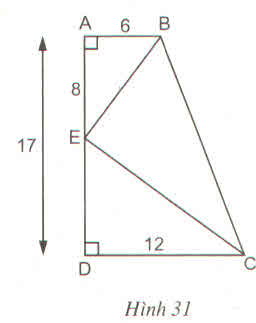
Cho hình thang vuông ABCD có Â=B=90⁰, AD=17cm. Gọi E là 1 điểm trên cạnh AD. Biết DE=10cm, EC=15cm, BE=9cm. Chứng minh tam giác BEC vuông
Cho tam giácABC có AB=8cm,AC=10cm và BC=14cm,phân giác AD,trên tia đối của tia DA lấy điểm I sao cho \(\widehat{BCI}=\widehat{BAD}\)
a)Tính BD,CD
b)Tính \(\frac{S_{ABD}}{S_{ACD}}\)
c)Chứng minh DB.DC=DI.DA
d)Chứng minh AB.AC-DB.DC=AD2
Cho hình thang ABCD(góc A=góc D=90 độ),AD=15cm,CD=9cm.Gọi M là một điểm trên cạnh AD,biết rằng MB=5cm,MC=15cm. a)Tam giác ABM đồng dạng tam giác DMC b)Gọi N là trung điểm của BC.Tính độ dài MN
Cho tam giác ABC (\(\widehat{A}=90^0\)) có đường cao AH (h.34).
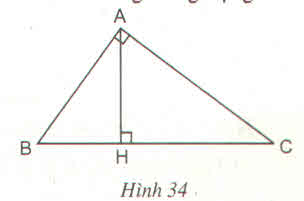
Chứng minh rằng : \(AH^2=BH.CH\)
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A, D ∈ BC. a) Tính DB/DC? b) Kẻ đường cao AH (H ∈ BC). Chứng minh rằng: AH/CH=AB/CA
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A, D ∈ BC. a) Tính DB/DC? b) Kẻ đường cao AH (H ∈ BC). Chứng minh rằng: AH/CH=AB/CA
GT: hcn ABCD, \(AH\perp BD\)
lấy \(E\in DH,K\in BC\) sao cho \(\dfrac{DE}{DH}=\dfrac{CK}{CB}\)
KL: a) \(\Delta ADE\sim\Delta ACK\)
b) \(\Delta AEK\sim\Delta ADC\)
c) \(\widehat{AEK}=90^0\)
Cho hình thang ABCD có \(\widehat{A}\)=\(\stackrel\frown{D}\)=90độ, cạnh AB = 4cm, cạnh CD =9cm.Tính độ dài BD biết rằng \(BD\perp BC\)
Cho hình thằng ABCD có AB//CD, hai đường chéo cắt nhau tại O. Biết AB=6cm, OA=3cm, OC=9cm, OD=12cm. Qua O kẻ đường thẳng song song với CD cắt hai cạnh AD và BC theo thứ tự là M và N.
a. Tính OB và CD
b. Chứng minh OA.OD=OB.OC
c. Chứng minh OM=ON