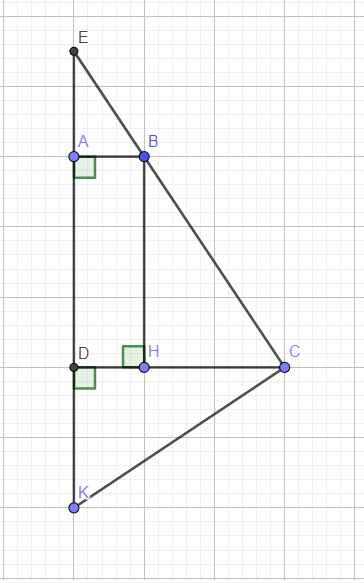
Do \(AD\perp CD\Rightarrow\) hình thang ABCD vuông tại A và D
\(\Rightarrow\) Tứ giác ABHD là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AD=BH\) \(\Rightarrow BH=CD\)
Xét hai tam giác vuông BCH và CKD có:
\(\left\{{}\begin{matrix}BH=CD\\DK=CH\end{matrix}\right.\) \(\Rightarrow\Delta BCH=\Delta CKD\left(c.g.c\right)\) (1)
\(\Rightarrow\widehat{DCK}=\widehat{HBC}\)
\(\Rightarrow\widehat{BCK}=\widehat{BCH}+\widehat{DCK}=\widehat{BCH}+\widehat{HBC}=90^0\)
\(\Rightarrow BC\perp CK\)
b. Cũng từ (1) ta suy ra \(CB=CK\)
Áp dụng hệ thức lượng trong tam giác vuông ECK với đường cao CD:
\(\dfrac{1}{CD^2}=\dfrac{1}{CE^2}+\dfrac{1}{CK^2}=\dfrac{1}{CE^2}+\dfrac{1}{CB^2}\) (đpcm)