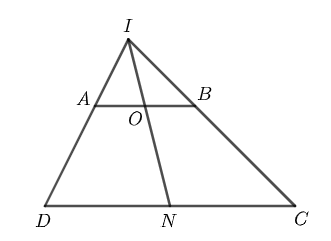
a) Do \(AB//CD\Rightarrow AO//DN\)
Áp dụng định lí Ta-let cho tam giác \(IDN\) ta có \(\dfrac{OI}{IN}=\dfrac{AO}{DN}\)
\(\Rightarrow OI.ND=OA.IN\)
b) Do \(AB//CD\Rightarrow BO//CN\)
Áp dụng định lí Ta-let cho tam giác \(ICN\) ta có \(\dfrac{OI}{IN}=\dfrac{BO}{CN}\)
\(\Rightarrow\dfrac{AO}{DN}=\dfrac{BO}{CN}\left(=\dfrac{OI}{IN}\right)\) mà \(DN=CN\) (do \(N\) là trung điểm \(CD\))
\(\Rightarrow AO=BO\Rightarrow O\) là trung điểm \(AB\)


