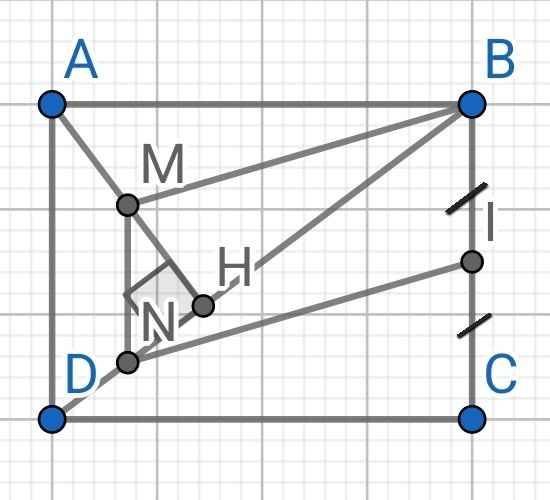
 a) Do M là trung điểm AH (gt)
a) Do M là trung điểm AH (gt)
N là trung điểm DH (gt)
⇒ MN là đường trung bình của ∆ADH
⇒ MN // AD
b) Do MN // AD
⇒ MN // BC
⇒ MN // BI
Do MN là đường trung bình của ∆ADH (cmt)
⇒ MN = AD : 2 (1)
Ta có:
I là trung điểm BC (gt)
⇒ BI = BC : 2 (2)
Do ABCD là hình chữ nhật (gt)
⇒ AD = BC (3)
Từ (1), (2) và (3) ⇒ MN = BI
Tứ giác BMNI có:
MN // BI (cmt)
MN = BI (cmt)
⇒ BMNI là hình bình hành
a: Xét ΔHAD có M,N lần lượt là trung điểm của HA, HD
=>MN là đường trung bình của ΔHAD
=>MN//AD và \(MN=\dfrac{AD}{2}\)
b; MN//AD
AD//BC
Do đó: MN//BC
\(MN=\dfrac{AD}{2}\)
\(AD=BC\)
\(BI=\dfrac{BC}{2}\)
Do đó: MN=BI
Xét tứ giác MNIB có
MN//IB
MN=IB
Do đó: MNIB là hình bình hành



