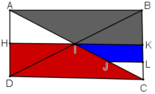
+ I là trung điểm AC; BD; HK
⇒ ĐI(H) = K ; ĐI(D) = B ; ĐI (C) = A.
⇒ Hình thang IKBA đối xứng với hình thang IHDC qua I (1)
+ J; L; K; I lần lượt là trung điểm của CI; CK; CB; CA
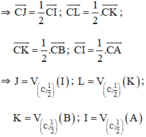
⇒ Hình thang JLKI là ảnh của hình thang IKBA qua phép vị tự tâm C tỉ số 1/2.
⇒ Hình thang JLKI là ảnh của hình thang IHDC qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm I và phép vị tự tâm C tỉ số 1/2.
⇒ IJKI và IHDC đồng dạng.

