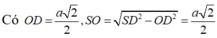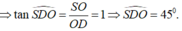Các câu hỏi tương tự
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng A.
2
2
B.
3
2
C.
2
3
D.
1
3
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
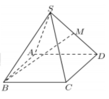
A. 2 2
B. 3 2
C. 2 3
D. 1 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng:
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng:
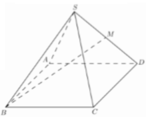
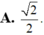

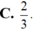
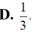
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là điểm trên đoạn SD sao cho SM2MD.Tan góc giữa đường thẳng BM và mặt phẳng (ABCD) là A.
1
3
B.
5
5
C.
3
3
D.
1
5
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là điểm trên đoạn SD sao cho SM=2MD.
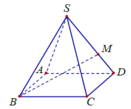
Tan góc giữa đường thẳng BM và mặt phẳng (ABCD) là
A. 1 3
B. 5 5
C. 3 3
D. 1 5
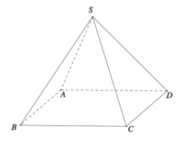
Cho hình chóp đều tứ giác đều S ABCD . có tất cả các cạnh bằng a . Gọi O là giao điểm AC và BD
a) Chứng minh SA vuông góc với SC.
b) Tính góc giữa mặt bên và mặt đáy.
c) Tính khoảng cách từ A đến mặt phẳng (SCD)
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn SO.
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác SCD (tham khảo hình vẽ bên). Tang góc giữa đường thẳng AG và mặt phẳng (ABCD) bằng A.
17
17
B.
2
5
5
C.
5...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác SCD (tham khảo hình vẽ bên). Tang góc giữa đường thẳng AG và mặt phẳng (ABCD) bằng
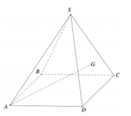
A. 17 17
B. 2 5 5
C. 5 5
D. 2 17 17
Cho hình chóp tứ giác đều SABCD có đáy ABCD là hình vuông tâm O các cạnh bên và các cạnh đáy đều bằng a Gọi M là trung điểm SC .Góc giữa 2 mặt phẳng MBD và ABCD bằng bao nhiêu?
Cho hình chóp S.ABCD có ABCD là hình vuông tâm O, cạnh a SA vuông góc với mặt phẳng (ABCD) và SA=a căn 2. Tính khoảng cách từ:
a) C đến mặt phẳng (SAB).
b) từ A đến (SCD).
c) Từ O đến (SCD).
d) Khoảng cách giữa hai đường thẳng AB và SC.
Cho hình chóp tứ giác đều có tất cả các cạnh bằng d. Gọi M là trung điểm của SD. O là giao điểm của hai đường chéo AC và BD. Tang của góc tạo bởi hai đường thẳng BM và SO là:
A
.
2
2
B
.
3
C
.
2
3
D
.
3
Đọc tiếp
Cho hình chóp tứ giác đều có tất cả các cạnh bằng d. Gọi M là trung điểm của SD. O là giao điểm của hai đường chéo AC và BD. Tang của góc tạo bởi hai đường thẳng BM và SO là:
A . 2 2
B . 3
C . 2 3
D . 3