a.
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(SA=SC=a\Rightarrow SA^2+SC^2=AC^2\)
\(\Rightarrow\Delta SAC\) vuông tại S (Pitago đảo)
\(\Rightarrow SA\perp SC\)
b.
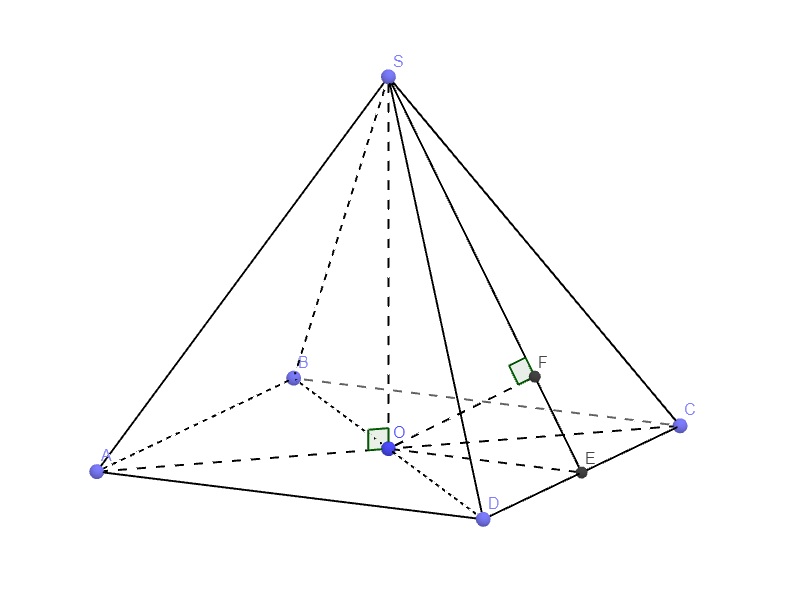
Gọi E là trung điểm CD \(\Rightarrow OE\perp CD\)
Chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\)
\(\Rightarrow CD\perp\left(SOE\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEO}\) là góc giữa mặt bên và đáy
\(OE=\dfrac{1}{2}BC=\dfrac{a}{2}\) (đường trung bình) ; \(SO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) (trung tuyến ứng với cạnh huyền)
\(\Rightarrow tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{2}\Rightarrow\widehat{SEO}=...\)
c.
Từ O kẻ \(OF\perp SE\Rightarrow OF\perp\left(SCD\right)\)
\(\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
Hệ thức lượng trong tam giác vuông SOE:
\(\dfrac{1}{OF^2}=\dfrac{1}{SO^2}+\dfrac{1}{OE^2}\Rightarrow OF=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{6}}{6}\)
\(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=2OF=\dfrac{a\sqrt{6}}{3}\)