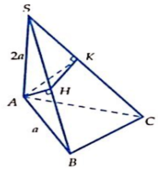
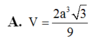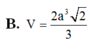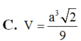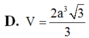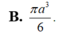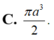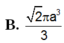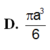\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow\Delta SAB\) vuông cân \(\Rightarrow\left\{{}\begin{matrix}SA=AB=a\\SB=a\sqrt{2}\end{matrix}\right.\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+2a^2}=a\sqrt{3}\)
\(\dfrac{V_{SAHIK}}{V_{SABCD}}=\dfrac{2V_{SAHI}}{2V_{SABC}}=\dfrac{V_{SAHI}}{V_{SABC}}=\dfrac{SH}{SB}.\dfrac{SI}{SC}=\left(\dfrac{SA}{SB}\right)^2\left(\dfrac{SA}{SC}\right)^2=\left(\dfrac{a}{a\sqrt{2}}\right)^2\left(\dfrac{a}{a\sqrt{3}}\right)^2=\dfrac{1}{6}\)
\(\Rightarrow V_{SAIHK}=\dfrac{1}{6}V_{SABCD}=\dfrac{1}{6}.\dfrac{1}{3}.SA.AB^2=\dfrac{a^3}{18}\)
Bạn coi lại đề, AHIK là 1 tứ giác nên ko thể có thể tích