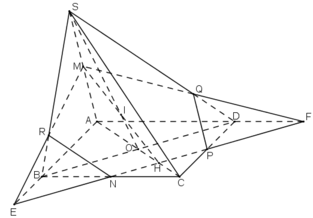
a) Tìm thiết diện :
Trong mp(ABCD), gọi F = AD ∩ PN và E = AB ∩ PN
Trong mp(SAD), gọi Q = MF ∩ SD
Trong mp(SAB), gọi R = ME ∩ SB
Nối PQ, NR ta được các đoạn giao tuyến của mp(MNP) với các mặt bên và mặt đáy của hình chóp là MQ, QP, PN, NR, RM
Vậy thiết diện cắt bởi mặt phẳng (MNP) là ngũ giác MQPNR.
b) Tìm SO ∩ (MNP). Gọi H là giao điểm của AC và PN .
Trong (SAC), SO ∩ MH = I
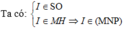
Vậy I = SO ∩ (MNP).

