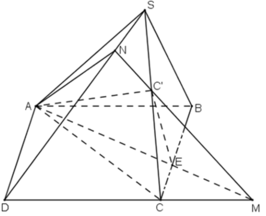
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE

