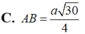a.
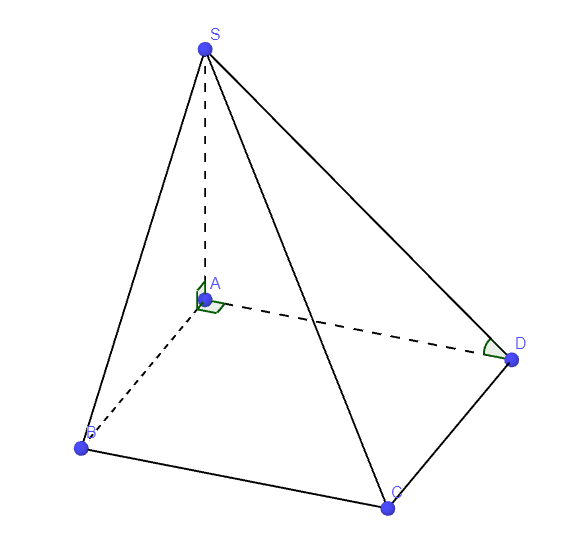
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD\in\left(SCD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
b.
Theo cmt: \(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp SD\\CD\perp AD\\CD=\left(SCD\right)\cap\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{SDA}\approx40^054'\)