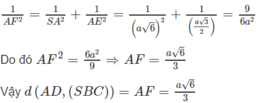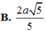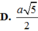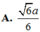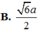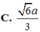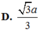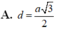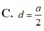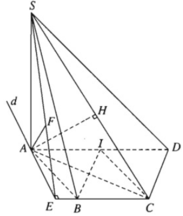
a) Vì ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a nên ta có: AD //BC và AB = BC = CD = a, đồng thời AC ⊥ CD, AB ⊥ BD, AC = BD = a√3.
Như vậy 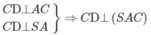
Trong mặt phẳng (SAC) dựng AH ⊥ SC tại H ta có AH ⊥ CD và AH ⊥ SC nên AH ⊥ (SCD)
Vậy AH = d(A,(SCD))
Xét tam giác SAC vuông tại A có AH là đường cao, ta có:
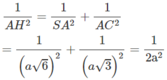
Vậy A H 2 = 2 a 2 ⇒ A H = a 2
Gọi I là trung điểm của AD ta có BI // CD nên BI song song với mặt phẳng (SCD). Từ đó suy ra d(B, (SCD)) = d(I,(SCD)).
Mặt khác AI cắt (SCD) tại D nên
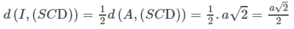
Do đó: 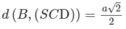
b) Vì AD // BC nên AD // (SBC), do đó d(AD, (SBC)) = d(A,(SBC))
Dựng AD ⊥ BC tại E ⇒ BC ⊥ (SAE)
Dựng AD ⊥ SE tại F ta có:
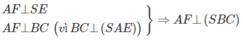
Vậy AF = d(A,(SBC)) = d(AD, (SBC))
Xét tam giác vuông AEB ta có:
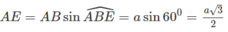
Xét tam giác SAE vuông tại A ta có: