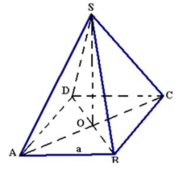
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng nhau. Khẳng định nào đúng?
A. Tâm mặt cầu ngoại tiếp hình chóp trùng với đỉnh S.
B. Tâm mặt cầu ngoại tiếp hình chóp là tâm của mặt đáy ABCD.
C. Tâm mặt cầu ngoại tiếp hình chóp là trung điểm của đoạn thẳng nối S với tâm của mặt đáy ABCD.
D. Tâm mặt cầu ngoại tiếp hình chóp là trọng tâm tam giác SAC.
Đáp án B
Phương pháp:
- Xác định tâm I của đáy, dựng đường (d) vuông góc với mặt đáy tại I
- Dựng mặt phẳng trung trực (P) của cạnh SA
- Xác định giao tuyến O của mặt phẳng (P) và đường thẳng (d). O chính là tâm mặt cầu ngoại tiếp hình chóp.
Cách giải:
Gọi O là tâm của đáy ⇒ OA = OB = OC = OD(1)
Do hình chóp có tất cả các cạnh đều bằng nhau nên ΔSAC = ΔBAC ⇒ OS = OA = OC(2)
Từ (1), (2) ⇒ OA = OB = OC = OD = OS ⇒ Tâm mặt cầu ngoại tiếp hình chóp là tâm của mặt đáy ABCD.

