Cho hàm số \(y=\left(m-3\right)x\)
a) Với giá trị nào của m thì hàm số đồng biến ? Nghoc
b) Xác định giá trị của m để đồ thị hàm số đi qua điểm \(A\left(1;2\right)\)
c) Xác định giá trị của m để đồ thị hàm số đi qua điểm \(B\left(1;-2\right)\)
d) Vẽ đồ thị của hai hàm số ứng với giá trị m tìm được ở câu b), c)
Lời giải
a) Hàm số bậc nhất đồng biến khi (a>0) => m-3 >0 => m>3
b) A(1;2) => y(1) =2 => (m-3).1=2 => m=5
c) B(1;-2) => y(1) =-2=> (m-3).1=-2 => m=1
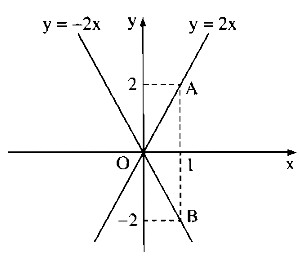
d) 
a) Hàm số \(y=\left(m-3\right)x\) đồng biến khi \(m-3>0\Leftrightarrow m>3\)
Hàm số \(y=\left(m-3\right)x\) nghịch biến khi \(m-3< 0\Leftrightarrow m< 3\)

ĐK: m - 3 # 0 <=> m # 0
a) * Hàm số đồng biến khi hệ số a = m - 3 > 0 <=> m > 3
Vậy với m > 3 thì hàm số
y=(m−3)xy=(m−3)x đồng biến.
* Hàm số nghịch biến khi hệ số a=m−3<0⇔m<3a=m−3<0⇔m<3
Vậy với m < 3 thì hàm số y = (m − 3) xy = (m − 3) x nghịch biến.
b) Đồ thị của hàm số y = (m − 3) xy = (m − 3) x đi qua điểm A(1;2) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có: 2 = (m − 3) 1 ⇔ 2 = m − 3 ⇔ m = 52 = (m − 3) 1 ⇔ 2 = m − 3 ⇔ m = 5.
Giá trị m = 5 thỏa mãn điều kiện bài toán .
Vậy với m = 5 thì đồ thị hàm số y = (m − 3) xy =(m − 3) x đi qua điểm A(1;2)
c) Đồ thị của hàm số y = (m − 3) xy = (m − 3) x đi qua điểm B(1;-2) nên tọa độ điểm B nghiệm đúng phương trình hàm số.
Ta có : −2 = (m − 3) 1 ⇔ −2 = m − 3 ⇔ m = 1 − 2 = (m − 3) 1 ⇔ − 2 = m − 3 ⇔ m = 1
Giá trị m = 1 thỏa mãn điều kiện bài toán .
Vậy với m = 1 thì đồ thị hàm số y = (m − 3) xy = (m − 3) x đi qua điểm B(1;-2).
d) Khi m = 5 thì ta có hàm số: y = 2x
Khi m = 1 thì ta có hàm số: y = -2x
*Vẽ đồ thị của hàm số y = 2x
Cho x = 0 thì y = 0. Ta có: O(0;0)
Cho x = 1 thì y = 2. Ta có: A(1;2)
Đường thẳng OA là đồ thị hàm số y = 2x.
*Vẽ đồ thị của hàm số
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = -2 . Ta có : B(1;-2)
Đường thẳng OB là đồ thị của hàm số y = -2x.