Cho góc xOY và tia Am (h.74a)
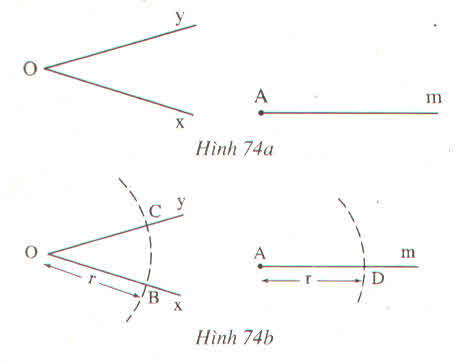
Vẽ cung tròn tâm O bán kính, cung này cắt Ox, Oy theo thứ tự ở B, C. Vẽ cung tròn tâm A bán kính r, cung này cắt tia Am ở D (h.74b)
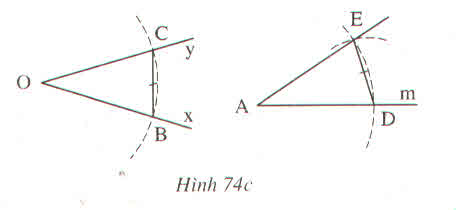
Vẽ cung tròn tâm D có bán kính bằng BC, cung này cắt cung tròn tâm A bán kính r ở E (h.74c)
Chứng minh rằng \(\widehat{DAE}=\widehat{xOy}\) ?
Tam giác DAE và BOC có:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
Nên ∆ DAE= ∆ BOC(c.c.c)
suy ra \(\widehat{DAE}\)=\(\widehat{BOC}\)(hai góc tương tứng)
vậy
\(\widehat{DAE}\)=\(\widehat{xOy}\).
-Tam giác DAE và tam giác BOC có:
AD = OB (gt)
AE = OC (gt)
DE = BC (gt)
Nên Tam giác DAE = BOC
Suy ra góc DAE = góc xOy (hai góc tương ứng)
Tam giác DAE và BOC có:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
Nên ∆ DAE= ∆ BOC(c.c.c)
suy ra \(\widehat{DAE}\)=\(\widehat{BOC}\)(hai góc tương tứng)
vậy
\(\widehat{DAE}\)=\(\widehat{xOy}\).
xét 2 tam giác DAE và BOC có
AD=OB(gt)
DE=BC(gt)
AE=BC(gt)
=>tam giác DAE=Tam giácBOC(c.c.c)
=>góc DAE=gocsBOC(góc T/U)
=>góc DAE=góc XOY
xong nhưng nó không cógóc nên mình ghi thế nhé
zúp mik vs ko chép mạng nhaaaaaaaaa